「その他 - ミラー効果とミラー容量」の版間の差分
ナビゲーションに移動
検索に移動
(ページの作成:「== 概要 == ミラー効果』と『ミラー容量』とは? 『ミラー効果』と『ミラー容量』とは? 上図の左に示すように、電圧利得-A倍…」) |
(→概要) |
||
| 1行目: | 1行目: | ||
== 概要 == | == 概要 == | ||
ここでは、ミラー効果とミラー容量について記載する。<br> | |||
<br><br> | |||
== ミラー効果とミラー容量とは == | |||
下図左に示すように、電圧利得-A倍の増幅器の入力と出力の間に容量Cが存在する場合を考える。<br> | |||
[[ファイル:Circuit Miller Effect 1.png|フレームなし|中央]] | |||
<br> | |||
この時、入力インピーダンスZ<sub>IN</sub>は、次式で表される。<br> | |||
<math>Z_{IN} = \frac{V_{IN}}{I_{IN}} = \frac{1}{j \omega (1 + A)C}</math><br> | |||
<br> | |||
これは、入力側から見ると、容量Cが等価的に(1 + A)倍になっているようにみえる。<br> | |||
これをミラー効果といい、大きくみえる容量のことをミラー容量という。<br> | |||
<br> | |||
<u>※補足</u><br> | |||
<u>ミラー効果(Miller Effect)は,1920年にJohn Milton Miller氏によって発表された現象である。</u><br> | |||
<br><br> | |||
== ミラー効果とミラー容量の式の導出方法 == | |||
増幅器の入出力インピーダンスが理想的であるとし、入力インピーダンスは無限大とする。<br> | |||
[[ファイル:Circuit Miller Effect 2.png|フレームなし|中央]] | |||
<br> | |||
この時、出力電圧V<sub>OUT</sub>と入力電圧V<sub>IN</sub>は、以下の2つの式で表される。<br> | |||
<math> | |||
\begin{cases} | |||
V_{OUT} &= -A V_{IN} \\ | |||
V_{IN} &= \frac{1}{C} \int I_{IN} dt + V_{OUT} | |||
\end{cases} | |||
</math><br> | |||
<br> | |||
上記の2式より、入力電圧V<sub>IN</sub>は次式となる。<br> | |||
<math>V_{IN} = \frac{1}{(1 + A)C} \int I_{IN} dt</math><br> | |||
<br> | |||
ここで、上式をラプラス変換すると、次式となる。<br> | |||
<math>V_{IN}(s) = \frac{1}{s(1+A)C} I_{IN}(s)</math><br> | |||
<math>\frac{V_{IN}(s)}{I_{IN}(s)} = \frac{1}{s(1 + A)C}</math><br> | |||
<br> | |||
次に、フーリエ変換を行って、sにjωを代入すると、入力インピーダンスZ<sub>IN</sub>は次式となる。<br> | |||
<math>Z_{IN} = \frac{V_{IN}}{I_{IN}} = \frac{1}{j \omega (1 + A)C}</math><br> | |||
<br> | |||
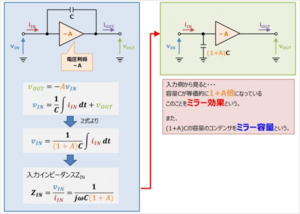
つまり、上図左の回路を入力側から見ると、(1 + A)Cの容量のコンデンサが並列に接続されている状態と等価となる。<br> | |||
そのため、上図右の等価回路に置き換えが可能となる。<br> | |||
<br> | |||
また、上図左の回路を入力側から見ると、容量Cが等価的に(1 + A)倍になっているように見える。<br> | |||
これをミラー効果といい、(1 + A)Cの容量(大きくみえる容量)のコンデンサをミラー容量という。<br> | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:電子回路]] | [[カテゴリ:電子回路]] | ||
2020年8月14日 (金) 11:01時点における最新版
概要
ここでは、ミラー効果とミラー容量について記載する。
ミラー効果とミラー容量とは
下図左に示すように、電圧利得-A倍の増幅器の入力と出力の間に容量Cが存在する場合を考える。
この時、入力インピーダンスZINは、次式で表される。
これは、入力側から見ると、容量Cが等価的に(1 + A)倍になっているようにみえる。
これをミラー効果といい、大きくみえる容量のことをミラー容量という。
※補足
ミラー効果(Miller Effect)は,1920年にJohn Milton Miller氏によって発表された現象である。
ミラー効果とミラー容量の式の導出方法
増幅器の入出力インピーダンスが理想的であるとし、入力インピーダンスは無限大とする。
この時、出力電圧VOUTと入力電圧VINは、以下の2つの式で表される。
上記の2式より、入力電圧VINは次式となる。
ここで、上式をラプラス変換すると、次式となる。
次に、フーリエ変換を行って、sにjωを代入すると、入力インピーダンスZINは次式となる。
つまり、上図左の回路を入力側から見ると、(1 + A)Cの容量のコンデンサが並列に接続されている状態と等価となる。
そのため、上図右の等価回路に置き換えが可能となる。
また、上図左の回路を入力側から見ると、容量Cが等価的に(1 + A)倍になっているように見える。
これをミラー効果といい、(1 + A)Cの容量(大きくみえる容量)のコンデンサをミラー容量という。