応用数学 - 広義積分と無限積分

概要

広義積分および無限積分について理解する。

極限の例題

例題:
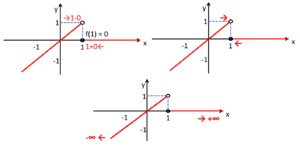
$f(x)={\begin{cases}x&\qquad (x<1)\\0&\qquad (x\geq 1)\end{cases}}$
について、以下の極限を求めよ。

(1) $\lim _{x\to 1+0}{f(x)}$
(2) $\lim _{x\to 1-0}{f(x)}$
(3) $\lim _{x\to 1}{f(x)}$
(4) $\lim _{x\to +\infty }{f(x)}$
(5) $\lim _{x\to -\infty }{f(x)}$

解答:
(1)
xを正の方向から1に近づけた極限なので、
$\lim _{x\to 1+0}{f(x)}=0$

(2)
xを負の方向から1に近づけた極限なので、
$\lim _{x\to 1-0}{f(x)}=1$

(3)
xを正と負の両方から近づけた極限である。
しかし、(1)(2)より、右側極限と左側極限は一致しない。
そのため、一定の値には収束しないので、
$\lim _{x\to 1}{f(x)}$ は値なし。

(4)
xを限りなく大きくしたときの極限なので、
$\lim _{x\to +\infty }{f(x)}=0\qquad ({\mbox{ 収 束 }})$

(5)
xを限りなく小さくしたときの極限なので、
$\lim _{x\to -\infty }{f(x)}=-\infty \qquad ({\mbox{ 発 散 }})$

連続な関数

定義:
関数 $f(x)$ が $x=a$ で連続とは、以下の条件を満たすことである。
(1) $f(a)$ が存在する。
(2) $\lim _{x\to a}{f(x)}$ が存在する。
(3) $\lim _{x\to a}{f(x)}=f(a)$

関数 $f(x)$ が区間Iで連続とは、以下の条件を満たすことである。
区間Iの任意の値aについて、$f(x)$ は $x=a$ で連続。

区分的に連続な関数

定義:
$a\leq x\leq b$ で定義された関数 $f(x)$ が以下の条件を満たすとき、 $f(x)$ は $a\leq x\leq b$ で区分的に連続(piecewisely continuous)であるという。

(1) $f(x)$ は $a\leq x\leq b$ において有限個の点を除いて連続である。
(2) $f(x)$ の不連続な点cにおいては、以下で示す右側極限と左側極限が存在する。
    $\lim _{x\to c+0}{f(x)}\qquad \lim _{x\to c-0}{f(x)}$

$f(x)$ が $a\leq x\leq b$ で区分的に連続であるとは、言い換えると以下の条件を満たすことである。
(1) 不連続な点があっても有限個である。
(2) 不連続な点では、値が $+\infty$ や $-\infty$ に発散したり振動したりしない。

このような区分的に連続な関数に対しては、連続な関数とほぼ同様に定積分を行うことができる。

下図に、区分的に連続な関数を示す。

図. $a\leq x\leq b$ において区分的に連続な関数 $f(x)$

ラプラス変換では、このような関数を扱う。

区分的に滑らかな関数

定義:
$a\leq x\leq b$ で定義された関数 $f(x)$ が以下の条件(1)(2)を全て満たすとき、 $f(x)$ は $a\leq x\leq b$ で区分的に滑らか(piecewisely smooth)であるという。

(1) $f(x)$ がこの区間において区分的に連続である。
(2) $f(x)$ の導関数 ${\frac {df(x)}{dx}}$ がこの区間において区分的に連続である。(ただし、 $f(x)$ に不連続点や、尖点がある場合、 ${\frac {df(x)}{dx}}$ はそれらの点を除いて考える)

広義積分

広義積分とは

定積分(definite integral)は、ある $x$ の区間 $a\leq x\leq b$ 上で連続な関数 $f(x)$ で考えていた。
ここでは、 $x=a$ や $x=b$ で $f(x)$ が発散してしまったり、定義されていない場合や、不連続の場合を考える。

このように、区間の端で不連続な $x$ にまで拡張された定積分を広義積分(improper integral)という。
また、広義積分が収束するとき、広義積分可能(improper integrable)であるという。

広義積分の定義

定義1:
$f(x)$ は $a<x\leq b$ で連続であるとする。
このとき、 $a<x\leq b$ における定積分を以下で定義する。

$\int _{a}^{b}{f(x)}\,dx=\lim _{\alpha \to a+0}{\int _{\alpha }^{b}{f(x)}\,dx}$

説明:
$a<\alpha \leq b$ となる $\alpha$ をとると、 $\alpha \leq x\leq b$ において $f(x)$ は連続なので、通常の定積分 $\int _{b}^{\alpha }{f(x)}\,dx$ が考えられる。
その結果を $\alpha \longrightarrow a+0$ として右側極限を考えたのが上の定義式である。
関数により、収束する場合もあり、収束しない場合もある。

定義2:
$f(x)$ は $a\leq x<b$ で連続であるとする。
このとき、 $a\leq x<b$ における定積分を以下で定義する。

$\int _{b}^{a}{f(x)}\,dx=\lim _{\beta \to b-0}{\int _{a}^{\beta }{f(x)}\,dx}$

定義3:
$f(x)$ は $a<x<b$ で連続であるとする。
このとき、 $a<x<b$ における定積分を以下で定義する。

$\int _{b}^{a}{f(x)}\,dx=\lim _{\begin{matrix}\alpha \to a+0\\\beta \to b-0\end{matrix}}{\int _{\alpha }^{\beta }{f(x)}\,dx}$

積分区間の分割

$f(x)$ が $a\leq x<c,\,c<x\leq b$ において連続で、 $x=c$ で不連続な場合、以下のように積分区間を分割して考えればよい。

${\begin{aligned}\int _{b}^{a}{f(x)\,dx}&=\int _{a}^{c}{f(x)\,dx}+\int _{c}^{b}{f(x)\,dx}\\&=\lim _{\gamma _{1}\to c-0}{\int _{a}^{\gamma _{1}}{f(x)\,dx}}+\lim _{\gamma _{2}\to c+0}{\int _{\gamma _{2}}^{b}{f(x)\,dx}}\end{aligned}}$

$f(x)$ が $a\leq x<c,\,c<x\leq b$ において連続で、 $x=c$ で不連続な場合、
$f(x)$ が $x=c$ で不連続であっても、$c$ に関する $f(x)$ の右側極限と左側極限の値が有限の値に収束する場合には、普通の積分と同じように計算することができる。

一方、それら右側積分や左側積分の値が $+\infty$ や $-\infty$ に発散したり、振動したりする場合には、広義積分の収束・発散を調べる必要がある。

下図に、積分区間の分割の概要を示す。

図. $a\leq x\leq b$ において区分的に連続な関数 $f(x)$