「回路計算 - コンデンサ」の版間の差分
| 119行目: | 119行目: | ||
\end{cases} | \end{cases} | ||
</math><br> | </math><br> | ||
<br><br> | |||
== 例題 == | |||
==== 例題 1 ==== | |||
下図のように、静電容量C<sub>1</sub>、C<sub>2</sub>、C<sub>3</sub>のコンデンサが接続されている回路がある。<br> | |||
スイッチSが開いている時、各コンデンサの電荷は全て0であった。<br> | |||
スイッチSを閉じた時,<math>C_1 = 5 \mbox{[μF]}</math>のコンデンサには<math>3.5 \times 10^{-4} \mbox{[C]}</math>の電荷が、<math>C_2 = 2.5 \mbox{[μF]}</math>のコンデンサには<math>0.5 \times 10^{-4} \mbox{[C]}</math>の電荷が充電された。<br> | |||
静電容量C<sub>3</sub>の値はいくらか。<br> | |||
[[ファイル:CircuitCalc Capacitor 9.jpg|フレームなし|中央]] | |||
<br> | |||
以下に解答を示す。<br> | |||
<br> | |||
C<sub>1</sub>にかかる電圧V<sub>1</sub>は、<math>Q_1 = C_1 V_1</math>より、<br> | |||
<math> | |||
\begin{align} | |||
3.5 \times 10^{-4} &= 5 \times 10^{-6} V_1 \\ | |||
V_1 &= 70 \mbox{[V]} | |||
\end{align} | |||
</math><br> | |||
<br> | |||
C<sub>2</sub>とC<sub>3</sub>にかかる電圧V<sub>2</sub>(C<sub>2</sub>とC<sub>3</sub>は並列接続されているので電圧V<sub>2</sub>は同じ値)は、<math>Q_2 = C_2 V_2</math>より、<br> | |||
<math> | |||
\begin{align} | |||
0.5 \times 10^{-4} &= 2.5 \times 10^{-6} V_2 \\ | |||
V_2 &= 20 \mbox{[V]} | |||
\end{align} | |||
</math><br> | |||
<br> | |||
C<sub>3</sub>の静電容量をx[uF]とすると、次式が成り立つ。<br> | |||
<math> | |||
\begin{align} | |||
\frac{V_2}{V_1 + V_2} &= \frac{C_1}{C_1 + (C2 + C3)} \\ | |||
\frac{20}{90} &= \frac{5}{5 + (2.5 + x)} \\ | |||
5 + 2.5 + x &= \frac{9}{2} \times 5 \\ | |||
x &= \frac{45}{2} - 7.5 \\ | |||
x &= 15 | |||
\end{align} | |||
</math><br> | |||
<br> | |||
したがって、C<sub>1</sub>の静電容量は15[uF]となる。<br> | |||
<br> | |||
==== 例題 2 ==== | |||
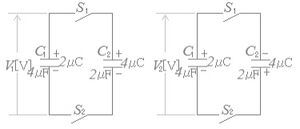
下図の左右のように,静電容量がそれぞれ4[μF]と2[μF]のコンデンサC<sub>1</sub>、C<sub>2</sub>、スイッチS<sub>1</sub>、S<sub>2</sub>からなる回路がある。<br> | |||
コンデンサC<sub>1</sub>とC<sub>2</sub>には,それぞれ2[μC]と4[μC]の電荷が下図のような極性で蓄えられている。<br> | |||
<br> | |||
この状態から両図ともスイッチS<sub>1</sub>およびS<sub>2</sub>を閉じる時、<br> | |||
下図左のコンデンサC<sub>1</sub>の端子電圧をV<sub>1</sub>[V]、下図右のコンデンサC<sub>2</sub>の端子電圧をV<sub>2</sub>[V]とすると、電圧比<math>\left| \frac{V_1}{V_2} \right|</math>の値はいくらか。<br> | |||
[[ファイル:CircuitCalc Capacitor 10.jpg|フレームなし|中央]] | |||
<br> | |||
以下に解答を示す。<br> | |||
<br> | |||
スイッチS<sub>1</sub>およびS<sub>2</sub>を閉じた時、<br> | |||
上図左では、合成容量<math>C_1 + C_2 = 6 \mbox{[μF]}</math>のコンデンサに合計<math>2 + 4 = 6 \mbox{[uC]}</math>の電荷が蓄えられていることになる。<br> | |||
<math>V_1 = \frac{6 \times 10^{-6}}{6 \times 10^{-6}} = 1 \mbox{[V]}</math><br> | |||
<br> | |||
上図右では、合成容量<math>C_1 + C_2 = 6 \mbox{[uF]}</math>のコンデンサに合計<math>2 - 4 = -2 \mbox{[uC]}</math>の電荷が蓄えられていることになる。<br> | |||
<math>V_2 = \frac{-2 \times 10^{-6}}{6 \times 10^{-6}} = - \frac{1}{3} \mbox{[V]}</math><br> | |||
<br> | |||
したがって、<math>\left| \frac{V_1}{V_2} \right| = 3</math>となる。 | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:回路計算]] | [[カテゴリ:回路計算]] | ||
2020年11月11日 (水) 03:58時点における版
概要
ここでは、コンデンサが1個の場合、直列接続の場合、並列接続の時のコンデンサの静電容量とコンデンサに蓄えられる電荷の基本的な考え方、計算方法について記載する。
1個のコンデンサ
コンデンサの静電容量
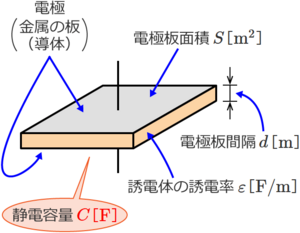
1個のコンデンサの静電容量は、下図のようにコンデンサの静電容量をC[F]、誘電体の誘電率をε[F/m]、電極板面積をS[m2]、電極板間隔をd[m]とすると、次式で与えられる。
… (1)
(1)式から、コンデンサの静電容量Cは、誘電体の誘電率εと電極板面積Sに比例し、電極板間隔dに反比例する。
したがって、コンデンサの静電容量Cは、誘電体の誘電率εまたは電極板面積Sが大きくなると大きくなり、電極板間隔dが大きくなると小さくなる。
コンデンサに蓄えられる電荷
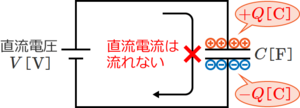
1個のコンデンサに直流電圧V[V]を印加すると、コンデンサは直流電流を流すことができないので回路に電流は流れないが、コンデンサには電荷が蓄えられる。
※備考
厳密に言えば、コンデンサに電荷が貯まりきるまでの時間であれば直流であっても電流は流れる。
この電荷が貯まりきるまでに流れる電流についての詳細は、RC直列回路の過渡現象のページを参照すること。
この時、蓄えられる電荷の大きさをQ[C]とすると、Qは次式で与えられる。
… (2)
(2)式を見ると、コンデンサに蓄えられる電荷Qは、コンデンサの静電容量Cとコンデンサにかかる電圧Vに比例する。
したがって、コンデンサに蓄えられる電荷Qは、コンデンサの静電容量Cまたはコンデンサにかかる電圧Vが大きくなると大きくなる。
コンデンサが直列接続されているときのコンデンサの静電容量と蓄えられる電荷
複数のコンデンサの静電容量
複数のコンデンサが直列接続されている時、コンデンサの静電容量(合成静電容量)は、
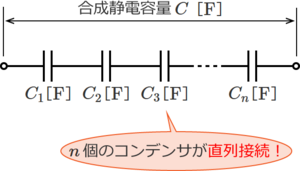
複数のコンデンサの静電容量をそれぞれ、C1[F]、C2[F] ... Cn[F]として直列接続すると下図のようになる。
このコンデンサの合成静電容量C[F]は、次式で与えられる。
複数のコンデンサに蓄えられる電荷
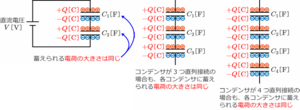
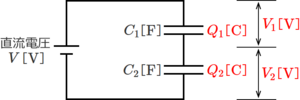
下図左のような2個のコンデンサが直列接続されている時、直流電圧V[V]を印加すると、コンデンサC1とC2には下図左のように電荷が蓄えられる。
この時、蓄えられる電荷の大きさは、C1とC2で同じ大きさになる。(直列接続されたコンデンサに蓄えられる電荷の大きさは同じ)
また、下図中央や下図右のように、コンデンサが3個、4個...と増えても、各コンデンサに蓄えられる電荷の大きさはどれも同じになる。
コンデンサC1、C2に蓄えられる電荷をそれぞれQ1、Q2、コンデンサC1、C2の電圧をそれぞれV1、V2とする。
下図から、連立方程式を立てて計算すると、コンデンサに蓄えられる電荷の大きさを求めることができる。
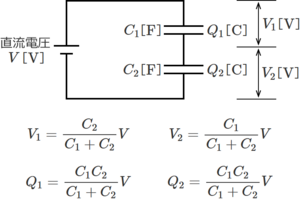
この回路の電源電圧をVとして、その電圧VがコンデンサC1とC2に分圧されるので、次式が成り立つ。
… (1)
次に、コンデンサC1の電圧はV1として、コンデンサの電荷の式Q = CVを当てはめると、(2)式となる。
同様にして、コンデンサC2にもコンデンサの電荷の式Q = CVを当てはめると、(3)式となる。
… (2)
… (3)
また、コンデンサが直列接続されている時、コンデンサに蓄えられる電荷の大きさはすべて同じになるので、(4)式が成り立つ。
… (4)
これらをまとめて、以下のように連立方程式にする。
(4)式を(3)式に代入して、代入した(3)式を(2)式に代入すると次式(5)となる。
(5)式を変形して、以下のようにする。
これを(1)式に代入すると、次式が求まる。
同様にして、V1は以下のようになる。
V1とV2が求められたので、(6)式と(7)式をそれぞれ(2)式と(3)式に代入して、Q1とQ2を求める。
コンデンサが並列接続されている時のコンデンサの静電容量と蓄えられる電荷
複数のコンデンサの静電容量
複数のコンデンサが並列接続されている時、コンデンサの静電容量(合成静電容量)は、
複数のコンデンサの静電容量をそれぞれ、C1[F]、C2[F] ... Cn[F]とすると下図のようになる。
このコンデンサの合成静電容量C[F]は、次式で与えられる。
複数のコンデンサに蓄えられる電荷
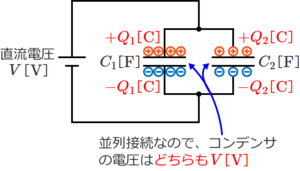
2個並列接続されているコンデンサに直流電圧V[V]を印加すると、コンデンサC1とC2には下図のように電荷が蓄えられる。
この時、コンデンサC1とC2の電圧は同じ大きさV[V]になる。
また、コンデンサが3個、4個...と増えても、各コンデンサの電圧の大きさはどれも同じになる。
例題
例題 1
下図のように、静電容量C1、C2、C3のコンデンサが接続されている回路がある。
スイッチSが開いている時、各コンデンサの電荷は全て0であった。
スイッチSを閉じた時,のコンデンサにはの電荷が、のコンデンサにはの電荷が充電された。
静電容量C3の値はいくらか。
以下に解答を示す。
C1にかかる電圧V1は、より、
C2とC3にかかる電圧V2(C2とC3は並列接続されているので電圧V2は同じ値)は、より、
C3の静電容量をx[uF]とすると、次式が成り立つ。
したがって、C1の静電容量は15[uF]となる。
例題 2
下図の左右のように,静電容量がそれぞれ4[μF]と2[μF]のコンデンサC1、C2、スイッチS1、S2からなる回路がある。
コンデンサC1とC2には,それぞれ2[μC]と4[μC]の電荷が下図のような極性で蓄えられている。
この状態から両図ともスイッチS1およびS2を閉じる時、
下図左のコンデンサC1の端子電圧をV1[V]、下図右のコンデンサC2の端子電圧をV2[V]とすると、電圧比の値はいくらか。
以下に解答を示す。
スイッチS1およびS2を閉じた時、
上図左では、合成容量のコンデンサに合計の電荷が蓄えられていることになる。
上図右では、合成容量のコンデンサに合計の電荷が蓄えられていることになる。
したがって、となる。
![{\displaystyle C=\epsilon {\frac {S}{d}}{\mbox{[F]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb03cb7061f63c4c4ad4b113c5c52532d6fb7f7c)
![{\displaystyle Q=CV{\mbox{[C]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74bd51bf69a0c969d2ae34357b7c25f84479eb54)
![{\displaystyle C={\frac {1}{{\frac {1}{C_{1}}}\times {\frac {1}{C_{2}}}\times {\frac {1}{C_{3}}}\times {\frac {1}{C_{4}}}\times \dots {\frac {1}{C_{n}}}}}[F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9d49e67c9097d3c33b492a8a8d3ff53f38a1b76)











![{\displaystyle C=C_{1}+C_{2}+C_{3}+\dots +C_{n}{\mbox{[F]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab8c5baf38e5839917e8dfcdf94c6e58b416d4f5)

![{\displaystyle C_{1}=5{\mbox{[μF]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a9e4fe9bf21a493276a32c5f96f45e494a6ed06)
![{\displaystyle 3.5\times 10^{-4}{\mbox{[C]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dce000cd8e5a6a7bea62e0f3dcefd2e4e98d7949)
![{\displaystyle C_{2}=2.5{\mbox{[μF]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/041f3ee781ed31258570d5b182890e6ecb0759d2)
![{\displaystyle 0.5\times 10^{-4}{\mbox{[C]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ad3ed6cfb1b43af23bccc604957d3627a0627ae)

![{\displaystyle {\begin{aligned}3.5\times 10^{-4}&=5\times 10^{-6}V_{1}\\V_{1}&=70{\mbox{[V]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddc2689fe8791fcb78f47aabcc166c2484f1e601)
![{\displaystyle {\begin{aligned}0.5\times 10^{-4}&=2.5\times 10^{-6}V_{2}\\V_{2}&=20{\mbox{[V]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8633853fdf44c06bd246e4f9d61ce9f3fd388)


![{\displaystyle C_{1}+C_{2}=6{\mbox{[μF]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1574a965bc24fffe8c3bb558df893970a966b976)
![{\displaystyle 2+4=6{\mbox{[uC]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84c902e91b0eec3cfa1b0ad8625327e7c1e2658)
![{\displaystyle V_{1}={\frac {6\times 10^{-6}}{6\times 10^{-6}}}=1{\mbox{[V]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13ab9a74f699bb2e9c5c375da0b8ea2c5bfdf562)
![{\displaystyle C_{1}+C_{2}=6{\mbox{[uF]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db773dcbe48e3b03672288ba423ba5b573c2a104)
![{\displaystyle 2-4=-2{\mbox{[uC]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eb48cae8d98b36dccbb47f984c46133599c2578)
![{\displaystyle V_{2}={\frac {-2\times 10^{-6}}{6\times 10^{-6}}}=-{\frac {1}{3}}{\mbox{[V]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57475d9a85450dddd51b22381cb46e660cb1b568)
