「ベクトル - ベクトル方程式」の版間の差分
| (同じ利用者による、間の17版が非表示) | |||
| 10行目: | 10行目: | ||
== 直線のベクトル方程式 == | == 直線のベクトル方程式 == | ||
==== | ==== 定点を通り、ある直線に平行な直線のベクトル方程式 ==== | ||
定点を通りある直線に平行な直線のベクトル方程式 | 定点を通りある直線に平行な直線のベクトル方程式 | ||
定点 <math>A(\vec{a})</math> を通り、<math>\vec{0}</math> でないベクトル <math>\vec{d}</math> に平行な直線のベクトル方程式 | 定点 <math>A(\vec{a})</math> を通り、<math>\vec{0}</math> でないベクトル <math>\vec{d}</math> に平行な直線のベクトル方程式 | ||
<math>\vec{p} = \vec{a} + t \vec{d}</math> | <math>\vec{p} = \vec{a} + t \vec{d}</math> | ||
<br> | |||
[[ファイル:Vector Equation 1.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
点 <math>A(\vec{a})</math> を通り、<math>\vec{0}</math> でないベクトル <math>\vec{d}</math> に平行な直線をgとする。<br> | 点 <math>A(\vec{a})</math> を通り、<math>\vec{0}</math> でないベクトル <math>\vec{d}</math> に平行な直線をgとする。<br> | ||
| 48行目: | 50行目: | ||
<math>m (x - x_1 ) - l (y - y_1) = 0</math> | <math>m (x - x_1 ) - l (y - y_1) = 0</math> | ||
<br> | <br> | ||
==== 異なる2点を通る直線のベクトル方程式(共線条件) ==== | ==== 異なる2点を通る直線のベクトル方程式(共線条件) ==== | ||
異なる2点を通る直線のベクトル方程式(共線条件)の定義 | 異なる2点を通る直線のベクトル方程式(共線条件)の定義 | ||
| 57行目: | 60行目: | ||
<br> | <br> | ||
平面上の異なる2点 <math>A(\vec{a}), \, B(\vec{b})</math> を通る直線上に,点 <math>P(\vec{p})</math> があることを考える。<br> | 平面上の異なる2点 <math>A(\vec{a}), \, B(\vec{b})</math> を通る直線上に,点 <math>P(\vec{p})</math> があることを考える。<br> | ||
[[ファイル:Vector Equation 2.jpg|フレームなし|中央]] | |||
<br> | |||
この時、<math>\overrightarrow{OP} = \overrightarrow{OA} + t \overrightarrow{AB}</math> と表されるので、次式となる。<br> | この時、<math>\overrightarrow{OP} = \overrightarrow{OA} + t \overrightarrow{AB}</math> と表されるので、次式となる。<br> | ||
<math> | <math> | ||
| 69行目: | 74行目: | ||
<br> | <br> | ||
例. <math>A(2, 1), \, B(3, 3)</math> の時、直線ABの式は <math>y = 2x - 3</math> である。<br> | 例. <math>A(2, 1), \, B(3, 3)</math> の時、直線ABの式は <math>y = 2x - 3</math> である。<br> | ||
[[ファイル:Vector Equation 3.jpg|フレームなし|中央]] | |||
<br> | |||
P(x, y)として、ベクトルで考えると<br> | P(x, y)として、ベクトルで考えると<br> | ||
<math> | <math> | ||
| 89行目: | 96行目: | ||
上記の連立方程式からtを消去すると、直線の式 <math>y = 2x - 3</math> が成り立つことがわかる。<br> | 上記の連立方程式からtを消去すると、直線の式 <math>y = 2x - 3</math> が成り立つことがわかる。<br> | ||
<br> | <br> | ||
==== | ==== 定点を通り、あるベクトルに垂直な直線のベクトル方程式 ==== | ||
定点を通り,ある直線に垂直な直線のベクトル方程式の定義 | 定点を通り,ある直線に垂直な直線のベクトル方程式の定義 | ||
| 97行目: | 104行目: | ||
<br> | <br> | ||
下図に、定点 <math>A(\vec{a})</math> を通り、ベクトル <math>\vec{n}</math> に垂直な直線を示す。<br> | 下図に、定点 <math>A(\vec{a})</math> を通り、ベクトル <math>\vec{n}</math> に垂直な直線を示す。<br> | ||
[[ファイル:Vector Equation 4.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
点 <math>P(\vec{p})</math> がこの直線上にあるということは、<math>\vec{n} \perp \overrightarrow{AP}</math> である。<br> | 点 <math>P(\vec{p})</math> がこの直線上にあるということは、<math>\vec{n} \perp \overrightarrow{AP}</math> である。<br> | ||
| 104行目: | 112行目: | ||
<br> | <br> | ||
例. 点 <math>A(2, 1), \, B(3, 3)</math> 、直線ABの式 <math>y = 2x - 3</math> とする時、この直線に垂直な直線の式を求める。<br> | 例. 点 <math>A(2, 1), \, B(3, 3)</math> 、直線ABの式 <math>y = 2x - 3</math> とする時、この直線に垂直な直線の式を求める。<br> | ||
P(x, y) | [[ファイル:Vector Equation 5.jpg|フレームなし|中央]] | ||
<br> | |||
P(x, y) として、ベクトルで考える。<br> | |||
<math>\overrightarrow{AP} \cdot \overrightarrow{A } = 0</math><br> | <math>\overrightarrow{AP} \cdot \overrightarrow{A } = 0</math><br> | ||
<math>\begin{pmatrix} x - 2 \\ y - 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = 0</math><br> | <math>\begin{pmatrix} x - 2 \\ y - 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = 0</math><br> | ||
| 115行目: | 125行目: | ||
== ベクトルの終点の存在範囲 == | == ベクトルの終点の存在範囲 == | ||
==== 定義 ==== | |||
ベクトルの終点の存在範囲の定義 | ベクトルの終点の存在範囲の定義 | ||
| 131行目: | 142行目: | ||
平行四辺形OACBの周と内部 | 平行四辺形OACBの周と内部 | ||
<math>\begin{cases} \vec{p} = s \vec{a} + t \vec{b} \\ 0 \le s \le 1 \\ 0 \le t \le 1 \\ \end{cases}</math> | <math>\begin{cases} \vec{p} = s \vec{a} + t \vec{b} \\ 0 \le s \le 1 \\ 0 \le t \le 1 \\ \end{cases}</math> | ||
<br> | |||
==== 直線AB ==== | |||
異なる2点を通る直線のベクトル方程式の通り、点 <math>P(\vec{p})</math> が次式を満たしながら動く時、点 <math>P(\vec{p})</math> の存在範囲は直線ABとなる。<br> | |||
[[ファイル:Vector Equation 2.jpg|フレームなし|中央]] | |||
<br> | |||
<math> | |||
\begin{cases} | |||
\vec{p} = s \vec{a} + t \vec{b} \\ | |||
s + t = 1 | |||
\end{cases} | |||
</math><br> | |||
<br> | |||
==== 線分AB ==== | |||
点 <math>P(\vec{p})</math> の存在範囲を線分AB上に限定する場合を考える。<br> | |||
[[ファイル:Vector Equation 7.jpg|フレームなし|中央]] | |||
<br> | |||
* <math>t = 0 (s = 1)</math> の時、点 <math>P(\vec{p})</math> は、点 <math>A(\vec{a})</math> と一致する。 | |||
* <math>t = 0.5 (s = 0.5)</math> の時、点 <math>P(\vec{p})</math> は、線分ABの中点に位置する。 | |||
* <math>t = 1 (s = 0)</math> の時、点 <math>P(\vec{p})</math> は、点 <math>B(\vec{b})</math> と一致する。 | |||
<br> | |||
つまり、<math>0 \le t \le 1 \, \, (0 \le s \le 1)</math> の時、線分ABを表現することができる。<br> | |||
<br> | |||
<math> | |||
\begin{cases} | |||
\vec{p} = s \vec{a} + t \vec{b} \\ | |||
s + t = 1 \\ | |||
s \ge 0 \\ | |||
t \ge 0 \\ | |||
\end{cases} | |||
\qquad | |||
\mbox{は 、 線 分 AB を 表 す } | |||
</math><br> | |||
<br> | |||
==== △OAB ==== | |||
例えば、<math>s + t = 0.5</math> の時、次式となり、<br> | |||
tを <math>0 \le t \le 0.5</math> の範囲で変化させると、点Pは、下図(1)のように、線分ABに平行な線分A'B'上を動く。<br> | |||
[[ファイル:Vector Equation 8.jpg|フレームなし|中央]] | |||
<br> | |||
<math> | |||
\begin{align} | |||
\vec{p} &= (0.5 - t) \vec{a} + t \vec{b} \\ | |||
&= 0.5 \vec{a} + t (\vec{b} - \vec{a}) \\ | |||
&= 0.5 \overrightarrow{OA} + t \overrightarrow{AB} | |||
\end{align} | |||
</math><br> | |||
<br> | |||
そして、<math>s + t</math> を、<math>0 \le s + t \le 1</math> の範囲で変化させると、線分A'B'は、上図(2)のように、△OABの全体を動く。<br> | |||
<br> | |||
したがって、<br> | |||
<math> | |||
\begin{cases} | |||
\vec{p} = s \vec{a} + t \vec{b} \\ | |||
0 \le s + t \le 1 \\ | |||
s \ge 0 \\ | |||
t \ge 0 \\ | |||
\end{cases} | |||
\qquad | |||
\mbox{は 、 △ OAB の 周 と 内 部 を 表 す } | |||
</math><br> | |||
<br> | |||
==== 平行四辺形OACB ==== | |||
例えば、<math>s = 0.5</math> の時、<math>\vec{p} = 0.5 \overrightarrow{OA} + t \overrightarrow{OB}</math> となり、<br> | |||
tを <math>0 \le t \le 1</math> の範囲で変化させる時、点Pは、下図(1)の線分OBに平行な線分A'C'上を動く。<br> | |||
[[ファイル:Vector Equation 6.jpg|フレームなし|中央]] | |||
<br> | |||
次に、sを <math>0 \le s \le 1</math> の範囲で変化させる時、上図(2)のように、線分A'C'は、線分OBから線分ACまで平行に動く。<br> | |||
<br> | |||
したがって、<br> | |||
<math> | |||
\begin{cases} | |||
\vec{p} = s \vec{a} + t \vec{b} \\ | |||
0 \le s \le 1 \\ | |||
0 \le t \le 1 \\ | |||
\end{cases} | |||
\qquad | |||
\mbox{は 、 平 行 四 辺 形 OACB の 周 と 内 部 を 表 す } | |||
</math> | |||
<br><br> | <br><br> | ||
== 円のベクトル方程式 == | == 円のベクトル方程式 == | ||
==== 中心がC,半径がrの円のベクトル方程式 ==== | |||
中心がC、半径がrの円のベクトル方程式の定義 | |||
3つの定点を <math>A(\vec{a}), B(\vec{b}), C(\vec{c})</math> 、円周上の任意の点を <math>P(\vec{p})</math> とする。 | |||
<math>|\vec{p} - \vec{c}| = r</math> | |||
または | |||
<math>(\vec{p} - \vec{c}) \cdot (\vec{p} - \vec{c}) = r^2</math> | |||
<br> | |||
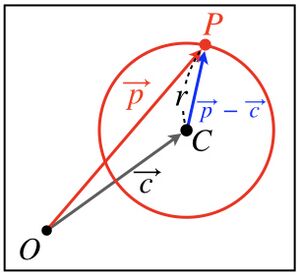
下図に示すように、中心C、半径rの円上にある点Pについて考える。<br> | |||
[[ファイル:Vector Equation 9.jpg|フレームなし|中央]] | |||
<br> | |||
円の定義は、"中心Cからの距離がrである点の集まり"であるため、<math>CP = r</math> である。<br> | |||
ベクトルで表すと、<math>| \overrightarrow{CP} | = r \quad \mbox{よ り } \quad | \vec{p} - \vec{c} | = r</math> である。<br> | |||
<br> | |||
ゆえに、<math>| \vec{p} - \vec{c} |^2 = r^2</math><br> | |||
したがって、<math>( \vec{p} - \vec{c} ) \cdot ( \vec{p} - \vec{c} ) = r^2</math><br> | |||
<br> | |||
また、<math>C(a, b), \, P(x, y)</math> として成分で表すと、<math>(x - a)^2 + (y - b)^2 = r^2</math> であり、円の方程式となる。<br> | |||
<br> | |||
* 例. 点C(3, 2)が中心で、点R(1, 1)が通る円 | |||
P(x, y)、O(0, 0)、C(3, 2)、R(1, 1)とする。<br> | |||
<math>| \overrightarrow{CP} | = | \overrightarrow{CR} |</math><br> | |||
<math>| \overrightarrow{OP} - \overrightarrow{OC} | = | \overrightarrow{OR} - \overrightarrow{OC} |</math><br> | |||
<br> | |||
<math>OP = (x, y), \, OC = (3, 2), \, OR = (1, 1)</math> より、<br> | |||
<math>| (x - 3, y - 2) | = | (-2, -1) |</math><br> | |||
<math>\sqrt{(x - 3)^2 + (y - 2)^2} = \sqrt{5}</math><br> | |||
<math>(x - 3)^2 + (y - 2)^2 = 5</math><br> | |||
<br> | |||
したがって、円の方程式は、<math>(x - 3)^2 + (y - 2)^2 = 5</math> となる。<br> | |||
<br> | |||
==== 直径がABの円のベクトル方程式 ==== | |||
円のベクトル方程式の定義 2 | |||
3つの定点を <math>A(\vec{a}), \, B(\vec{b})</math> 、円周上の任意の点を <math>P(\vec{p})</math> とする。 | |||
<math>(\vec{p} - \vec{a}) \cdot (\vec{p} - \vec{b}) = 0</math> | |||
<br> | |||
下図に示すように、直径がABの円周上の点Pについて考える。<br> | |||
[[ファイル:Vector Equation 10.jpg|フレームなし|中央]] | |||
<br> | |||
直径に対する円周角は直角であるから、<math>AP \perp BP</math> であり、 <math>\overrightarrow{AP} \cdot \overrightarrow{BP} = 0</math> となる。<br> | |||
したがって、次式となる。<br> | |||
<math>(\overrightarrow{OP} - \overrightarrow{OA}) \cdot (\overrightarrow{OP} - \overrightarrow{OB}) = 0</math><br> | |||
<math>\therefore (\vec{p} - \vec{a}) \cdot (\vec{p} - \vec{b}) = 0</math><br> | |||
<br> | |||
* 例1. 円の中心がC(3. 2)で、点R(1, 1)を通る円 | |||
*: 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、 | |||
*: <math>| \overrightarrow{CP} | = | \overrightarrow{CR} |</math> | |||
*: <math>| \overrightarrow{OP} - \overrightarrow{OC} | = | \overrightarrow{OR} - \overrightarrow{OC} |</math> | |||
*: <br> | |||
*: <math>\overrightarrow{OP} = (x, y), \, \overrightarrow{OC} = (3 , 2), \, \overrightarrow{OR} = (1, 1)</math> より、 | |||
*: <math>| (x - 3, y - 2) | = | (-2, -1) |</math> | |||
*: <math>\sqrt{(x - 3)^2 + (y - 2)^2} = \sqrt{5}</math> | |||
*: <math>(x - 3)^2 + (y - 2)^2 = 5</math> | |||
*: <br> | |||
*: したがって、<math>(x - 3)^2 + (y - 2)^2 = 5</math> となる。 | |||
*: <br> | |||
* 例2. 点A(2, 5)と点B(4, 1)を直径の両端とする円 | |||
*: 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、 | |||
*: <math>\overrightarrow{AP} \cdot \overrightarrow{BP} = 0 \qquad \because \overrightarrow{AP} \bot \overrightarrow{BP}</math> | |||
*: <math>(\overrightarrow{OP} - \overrightarrow{OA}) \cdot (\overrightarrow{OP} - \overrightarrow{OB}) = 0</math> | |||
*: <br> | |||
*: <math>\overrightarrow{OP} = (x, y), \, \overrightarrow{OA} = (2 , 5), \, \overrightarrow{OB} = (4, 1)</math> より、 | |||
*: <math>(x - 2, y - 5) \cdot (x - 4, y - 1) = 0</math> | |||
*: <math>x^2 - 6x + y^2 - 6y + 13 = 0</math> | |||
*: <math>(x - 3)^2 - 9 + (y - 3)^2 - 9 = -13</math> | |||
*: <math>(x - 3)^2 + (y - 3)^2 = 5</math> | |||
*: <br> | |||
*: したがって、<math>(x - 3)^2 + (y - 3)^2 = 5</math> となる。 | |||
<br> | |||
==== 円の接線のベクトル方程式 ==== | |||
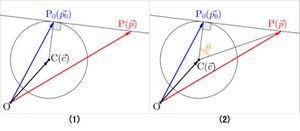
下図(1)のように、円の中心点 <math>C(\vec{c})</math>、円周上の接点を <math>P_0(\vec{p_0})</math> とする時、接線上の点 <math>P(\vec{p})</math> の位置ベクトルは、次式となる。<br> | |||
[[ファイル:Vector Equation 11.jpg|フレームなし|中央]] | |||
<br> | |||
<math>\overrightarrow{P_0 P} \cdot \overrightarrow{CP_0} = 0</math><br> | |||
<math>( \overrightarrow{p} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> | |||
<br> | |||
また、下図(2)より、<math>| \overrightarrow{CP} | \cos{\theta} = | \overrightarrow{CP_0} |</math><br> | |||
<br> | |||
両辺に、<math>| \overrightarrow{CP_0} |</math> を乗算すると、<br> | |||
<math>| \overrightarrow{CP} | | \overrightarrow{CP_0} | \cos{\theta} = | \overrightarrow{CP_0} |^2</math><br> | |||
<math>\overrightarrow{CP} \cdot \overrightarrow{CP_0} = r^2</math><br> | |||
<br> | |||
したがって、<math>( \overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = r^2 \qquad (1)</math> となる。<br> | |||
<br> | |||
(1)式は、次のようにしても求めることができる。<br> | |||
<math>( \overrightarrow{p} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> | |||
<math>( \overrightarrow{p} - \overrightarrow{c} + \overrightarrow{c} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> | |||
これを展開する。<br> | |||
<math> | |||
\begin{align} | |||
(\overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) &= ( \overrightarrow{p_0} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) \\ | |||
&= | \overrightarrow{p_0} - \overrightarrow{c} |^2 \\ | |||
&= r^2 | |||
\end{align} | |||
</math><br> | |||
<br> | |||
点Pの位置ベクトルを <math>P(\vec{p}) = (x, y)</math>、円の中心Cの位置ベクトル <math>C(\vec{c}) = (a, b)</math>、接点P<sub>0</sub>の位置ベクトル <math>P_0(\vec{p_0}) = (x_0, y_0)</math> とする。<br> | |||
<math>( \overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) =r^2</math><br> | |||
<math>(x - a, y - b) \cdot (x_0 - a, y_0 - b) = r^2</math><br> | |||
<math>(x_0 - a)(x - a) + (y_0 - b)(y - b) = r^2</math><br> | |||
<br> | |||
これは、円の接線の方程式を表していることが分かる。<br> | |||
<br> | |||
* 例. 円の中心 <math>C(1, 1)</math>、半径 <math>\sqrt{2}</math> の円に、<math>P(2, 2)</math> で接する接線の方程式をベクトルを用いて求めよ。 | |||
*: <math>\overrightarrow{OC} = (1, 1), \, \overrightarrow{OA} = (2, 2), \, \overrightarrow{OP} = (x, y)</math> とする。 | |||
*: <math>\overrightarrow{AP} \cdot \overrightarrow{AC} = 0 \quad \Longrightarrow \quad (\vec{p} - \vec{a}) \cdot (\vec{c} - \vec{a}) = 0</math> より、 | |||
*: <math>(x - 2, y - 2) \cdot (1, 1) = x - 2 + y - 2 = x - y - 4 = 0</math> | |||
*: <math>\therefore y = -x + 4</math> | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:解析学]] | [[カテゴリ:解析学]] | ||
2024年1月9日 (火) 10:41時点における最新版
概要
ベクトル方程式とは、"ある条件を満たす点を、ベクトルで表現した式"のことである。
直線は、点の集合である。
例えば,直線 は、点(x, y)が満たす条件を式にしたもので,この条件を満たす点の集合が直線になる。
ベクトルでは、点の位置を表すために、位置ベクトルが存在する。
この位置ベクトルを利用して、曲線上の点の位置ベクトル の満たす関係式を、その曲線のベクトル方程式という。
直線のベクトル方程式
定点を通り、ある直線に平行な直線のベクトル方程式
定点を通りある直線に平行な直線のベクトル方程式 定点 を通り、 でないベクトル に平行な直線のベクトル方程式
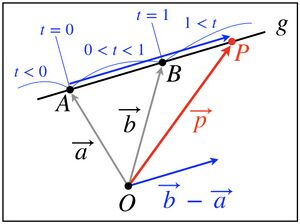
点 を通り、 でないベクトル に平行な直線をgとする。
点 が直線g上にあるということは、 と表すことができる。
より、
と表すことができる。
この時、 を直線gの方向ベクトルtを媒介変数という。
また、このベクトル方程式をベクトルの成分で表すことを考える。
原点をO、点Aの座標を 、直線g上の任意の点を として、 とする時、
ベクトル方程式は、次式となる。
媒介変数tを用いて表されたこの連立方程式を、直線gの媒介変数表示という。
この連立方程式からtを消去する時、次のことが成り立つ。
点 を通り、 が方向ベクトルである直線の方程式
異なる2点を通る直線のベクトル方程式(共線条件)
異なる2点を通る直線のベクトル方程式(共線条件)の定義 異なる2点 を通る直線のベクトル方程式は、次式となる。 または
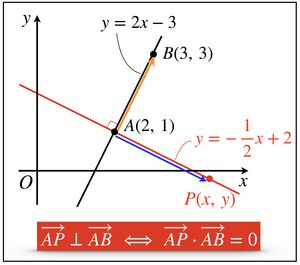
平面上の異なる2点 を通る直線上に,点 があることを考える。
この時、 と表されるので、次式となる。
上式の方程式において、 とおく時、次式としても表すことができる。
例. の時、直線ABの式は である。
P(x, y)として、ベクトルで考えると
したがって、次式のように媒介変数表示で表すことができる。
上記の連立方程式からtを消去すると、直線の式 が成り立つことがわかる。
定点を通り、あるベクトルに垂直な直線のベクトル方程式
定点を通り,ある直線に垂直な直線のベクトル方程式の定義 定点 を通り、 でないベクトル に垂直な直線のベクトル方程式 ( は直線の法線ベクトル)
下図に、定点 を通り、ベクトル に垂直な直線を示す。
点 がこの直線上にあるということは、 である。
内積を用いて表すと、次式となる。
例. 点 、直線ABの式 とする時、この直線に垂直な直線の式を求める。
P(x, y) として、ベクトルで考える。
したがって、ベクトル方程式 を用いて、定点 を通り、ベクトル に垂直な直線を表すことができる。
ベクトルの終点の存在範囲
定義
ベクトルの終点の存在範囲の定義 とする。(s、tは実数の変数) s、tに条件がある時,次のような図形を表す。 直線AB 線分AB の周と内部 平行四辺形OACBの周と内部
直線AB
異なる2点を通る直線のベクトル方程式の通り、点 が次式を満たしながら動く時、点 の存在範囲は直線ABとなる。
線分AB
点 の存在範囲を線分AB上に限定する場合を考える。
- の時、点 は、点 と一致する。
- の時、点 は、線分ABの中点に位置する。
- の時、点 は、点 と一致する。
つまり、 の時、線分ABを表現することができる。
△OAB
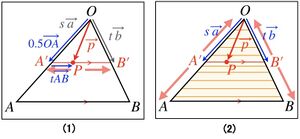
例えば、 の時、次式となり、
tを の範囲で変化させると、点Pは、下図(1)のように、線分ABに平行な線分A'B'上を動く。
そして、 を、 の範囲で変化させると、線分A'B'は、上図(2)のように、△OABの全体を動く。
したがって、
平行四辺形OACB
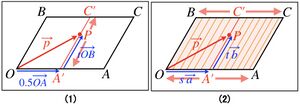
例えば、 の時、 となり、
tを の範囲で変化させる時、点Pは、下図(1)の線分OBに平行な線分A'C'上を動く。
次に、sを の範囲で変化させる時、上図(2)のように、線分A'C'は、線分OBから線分ACまで平行に動く。
したがって、
円のベクトル方程式
中心がC,半径がrの円のベクトル方程式
中心がC、半径がrの円のベクトル方程式の定義 3つの定点を 、円周上の任意の点を とする。 または
下図に示すように、中心C、半径rの円上にある点Pについて考える。
円の定義は、"中心Cからの距離がrである点の集まり"であるため、 である。
ベクトルで表すと、 である。
ゆえに、
したがって、
また、 として成分で表すと、 であり、円の方程式となる。
- 例. 点C(3, 2)が中心で、点R(1, 1)が通る円
P(x, y)、O(0, 0)、C(3, 2)、R(1, 1)とする。
より、
したがって、円の方程式は、 となる。
直径がABの円のベクトル方程式
円のベクトル方程式の定義 2 3つの定点を 、円周上の任意の点を とする。
下図に示すように、直径がABの円周上の点Pについて考える。
直径に対する円周角は直角であるから、 であり、 となる。
したがって、次式となる。
- 例1. 円の中心がC(3. 2)で、点R(1, 1)を通る円
- 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、
- より、
- したがって、 となる。
- 例2. 点A(2, 5)と点B(4, 1)を直径の両端とする円
- 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、
- より、
- したがって、 となる。
円の接線のベクトル方程式
下図(1)のように、円の中心点 、円周上の接点を とする時、接線上の点 の位置ベクトルは、次式となる。
また、下図(2)より、
両辺に、 を乗算すると、
したがって、 となる。
(1)式は、次のようにしても求めることができる。
これを展開する。
点Pの位置ベクトルを 、円の中心Cの位置ベクトル 、接点P0の位置ベクトル とする。
これは、円の接線の方程式を表していることが分かる。
- 例. 円の中心 、半径 の円に、 で接する接線の方程式をベクトルを用いて求めよ。
- とする。
- より、