極座標

概要

極座標とは、n次元ユークリッド空間Rn上で定義され、1個の動径rとn − 1個の偏角θ1, ..., θn−1からなる座標系のことである。
点S(0, 0, x3, ..., xn)を除く直交座標は、局所的に一意的な極座標に座標変換できるが、
点Sにおいては、ヤコビアンが0となってしまうため、一意的な極座標表現は不可能である。
これは、点Sにおける偏角が定義できないことからも明らかである。

円座標

2次元ユークリッド空間R2における極座標は円座標と呼ばれ、1つの動径座標と一つの角度座標からなる最も単純な極座標である。
rθ平面、極座標平面(または平面極座標)ともいう。

特異点は(r, θ) = (0, θ)、すなわち、xy座標での原点(x, y) = (0, 0)である。
2次元ベクトル空間にも定義できることから、複素数体C上にも定義できる。この時、円座標を極形式と呼んだりもする。
その場合、オイラーの公式を利用してz = reiθと表す。
円座標平面上で偏角を限定しない場合、xy平面上で円を描く。

円座標(r, θ)から直交直線座標(x, y)への変換は次式で与えられる。
${\begin{cases}x&=r\cos \theta \\y&=r\sin \theta \\\end{cases}}$

角度座標の範囲を$-\pi <\theta \leq \pi$とする場合、直交直線座標から円座標への変換は次式で与えられる。
ここで、sgnは符号関数である。
${\begin{cases}r&={\sqrt {x^{2}+y^{2}}}\\\theta &=\operatorname {sgn} (y)\cos ^{-1}\left({\frac {x}{\sqrt {x^{2}+y^{2}}}}\right)\\\end{cases}}$

原点(x,y) = (0,0)において、特異性があり、分母が0となるためθが定まらない。

ヤコビアン

2重積分に応用するには、変数変換を行うことにより、ヤコビアンを計算してdxdyとdrdθの関係式を求める必要がある。
${\begin{aligned}J&={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}\end{vmatrix}}\\&={\begin{vmatrix}\cos {\theta }&-r\sin {\theta }\\\sin {\theta }&r\cos {\theta }\end{vmatrix}}\\&=r\cos ^{2}{\theta }+r\sin ^{2}{\theta }\\&=r\end{aligned}}$
したがって、$dxdy=rdrd\theta$となる。

例1. 円の積分

以下の2重積分を求めよ。
$\iint \limits _{D}xy\ dxdy\qquad D=\{(x,y)|1\leq x^{2}+y^{2}\leq 4,\ x\geq 0,\ y\geq 0\}$

このように円が含まれる場合は、極座標変換 $x=r\cos {\theta },\,y=r\sin {\theta }(r\geq 0,\,0\leq \theta \leq 2\pi )$とおく。
積分範囲は、$1\leq r^{2}\leq 4,\,r\cos {\theta }\geq 0,\,r\sin {\theta }\geq 0$となり、$r\geq 0$のため、$1\leq r\leq 2,\,\cos {\theta }\geq 0,\,\sin {\theta }\geq 0$となる。
$\cos {\theta }\geq 0$かつ$\sin {\theta }\geq 0$を満たすθは、$0\leq \theta \leq {\frac {\pi }{2}}$なので、
変換後の積分範囲D'は、$D'=\{(r,\theta )|1\leq r\leq 2,\ 0\leq \theta \leq {\frac {\pi }{2}}\}$の形に変形でき、2重積分を計算することができる。
${\begin{aligned}&\iint _{D}xy\ dxdy\\=&\iint _{D'}r^{3}\sin {\theta }\cos {\theta }\ drd\theta \\=&\int _{1}^{2}r^{3}\ dr\int _{0}^{\frac {\pi }{2}}\sin {\theta }\cos {\theta }\ d\theta \\=&\int _{1}^{2}r^{3}\ dr\ {\frac {1}{2}}\int _{0}^{\frac {\pi }{2}}\sin {2\theta }\ d\theta \\=&\left[{\frac {1}{4}}r^{4}\right]_{1}^{2}\ {\frac {1}{2}}\left[-{\frac {1}{2}}\cos 2\theta \right]_{0}^{\frac {\pi }{2}}\\=&(4-{\frac {1}{4}})\ {\frac {1}{2}}({\frac {1}{2}}+{\frac {1}{2}})\\=&{\frac {15}{4}}\times {\frac {1}{2}}\\=&{\frac {15}{8}}\end{aligned}}$

例2. 楕円の積分

以下の2重積分を求めよ。
$\iint \limits _{D}xy\ dxdy\qquad D=\{(x,y)|{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}\leq 1,\ x\geq 0,\ y\geq 0\}$

積分領域Dが楕円の場合、楕円の方程式${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$の分母a²とb²を消すため、極座標変換を行い、
$x=ar\cos {\theta },\ y=br\sin {\theta }\ (r\geq 0,\ 0\leq \theta \leq 2\pi )$とおく。

ヤコビアンを計算して dxdyとdrdθの関係式を求める。
${\begin{aligned}J&={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}\end{vmatrix}}\\&={\begin{vmatrix}a\cos {\theta }&-ar\sin {\theta }\\b\sin {\theta }&br\cos {\theta }\end{vmatrix}}\\&=abr\cos ^{2}{\theta }+abr\sin ^{2}{\theta }\\&=abr\end{aligned}}$
したがって、$dxdy=abrdrd\theta$となる。

また、積分範囲は、$0\leq r^{2}\leq 1,\ r\cos {\theta }\geq 0,\ r\sin {\theta }\geq 0$となるので、
変換後の積分領域D'は、$D'=\{(r,\theta )|0\leq r\leq 1,\ 0\leq \theta \leq {\frac {\pi }{2}}\}$の形に変形できる。

${\begin{aligned}&\iint _{D}y\ dxdy\\=&\iint _{D'}ab^{2}r^{2}\sin {\theta }\ drd\theta \\=&ab^{2}\int _{0}^{1}r^{2}\ dr\ \int _{0}^{\frac {\pi }{2}}\sin {\theta }\ d\theta \\=&ab^{2}\left[{\frac {1}{3}}r^{3}\right]_{0}^{1}\left[-\cos \theta \right]_{0}^{\frac {\pi }{2}}\\=&ab^{2}{\frac {1}{3}}\times 1\\=&{\frac {1}{3}}ab^{2}\end{aligned}}$

円柱座標

円座標で(0, 0)を除くXY平面上の全ての点を表現できることから、これにZ軸を加えれば、XYZ空間が表現できる。
これを円柱座標という。

円柱座標空間上(RθZ空間上)で、θとZを限定しない場合、XYZ空間上で円柱を描く。
また、円柱座標空間上の特異点はZ軸上の全ての点である。

円筒座標(r, θ, z) から直交直線座標(x, y, z)への変換は次式で与えられる。
${\begin{cases}x&=r\cos \theta \\y&=r\sin \theta \\z&=z\end{cases}}$

直交直線座標から円筒座標への変換は、次式で与えられる。
${\begin{cases}r&={\sqrt {x^{2}+y^{2}}}\\\theta &=\operatorname {sgn} (y)\cos ^{-1}\left({\frac {x}{\sqrt {x^{2}+y^{2}}}}\right)\\z&=z\end{cases}}$

球座標

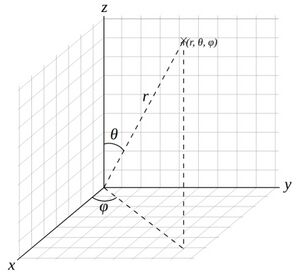
3次元ユークリッド空間R3における極座標である。球面座標ともいう。
1個の動径rと2個の偏角θ、φによって表現される。(下図を参照)

球座標において、動径を固定して、2個の偏角を動かせば、XYZ空間上で球を描く。

球座標から直交直線座標への変換は、次式で与えられる。
${\begin{cases}x&=r\sin \theta \cos \phi \\y&=r\sin \theta \sin \phi \\z&=r\cos \theta \\\end{cases}}$

直交直線座標から球座標への変換は、次式で与えられる。
${\begin{cases}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos \left({\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\right)\\\phi &=\operatorname {sgn} (y)\arccos \left({\frac {x}{\sqrt {x^{2}+y^{2}}}}\right)\end{cases}}$

Z軸上の$(x,y)=(0,0)$において特異性があり、分母が0となるためφが定まらない。
原点においては、θも定まらない。

ヤコビアンにおいて、$dxdydz$ と $drd\theta d\phi$ の関係式は次式となる。
${\begin{aligned}J&={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}&{\frac {\partial x}{\partial \phi }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}&{\frac {\partial y}{\partial \phi }}\\{\frac {\partial z}{\partial r}}&{\frac {\partial z}{\partial \theta }}&{\frac {\partial z}{\partial \phi }}\\\end{vmatrix}}\\&={\begin{vmatrix}\sin \theta \cos \phi &r\cos \theta \cos \phi &-r\sin \theta \sin \phi \\\sin \theta \sin \phi &r\cos \theta \sin \phi &r\sin \theta \cos \phi \\\cos \theta &-r\sin \theta &0\\\end{vmatrix}}\\&=r^{2}\sin \theta \cos ^{2}\theta \cos ^{2}\phi +r^{2}\sin ^{3}\theta \sin ^{2}\phi +r^{2}\sin \theta \cos ^{2}\theta \sin ^{2}\phi +r^{2}\sin ^{3}\theta \cos ^{2}\phi \\&=r^{2}(\sin \theta \cos ^{2}\theta \cos ^{2}\phi +\sin ^{3}\theta \sin ^{2}\phi +\sin \theta \cos ^{2}\theta \sin ^{2}\phi +\sin ^{3}\theta \cos ^{2}\phi )\\&=r^{2}\left\{\sin ^{3}\theta (\sin ^{2}\phi +\cos ^{2}\phi )+\sin \theta \cos ^{2}\theta (\sin ^{2}\phi +\cos ^{2}\phi )\right\}\\&=r^{2}(\sin ^{3}\theta +\sin \theta \cos ^{2}\theta )\\&=r^{2}\sin \theta (\sin ^{2}\theta +\cos ^{2}\theta )\\&=r^{2}\sin \theta \end{aligned}}$

したがって、$dxdydz=r^{2}\sin \theta \,drd\theta d\phi$ となる。