|
|
| (同じ利用者による、間の13版が非表示) |
| 10行目: |
10行目: |
|
| |
|
| == 直線のベクトル方程式 == | | == 直線のベクトル方程式 == |
| ==== 定点 <math>A(\vec{a})</math> を通り、<math>\vec{d}</math> に平行な直線のベクトル方程式 ==== | | ==== 定点を通り、ある直線に平行な直線のベクトル方程式 ==== |
| 定点を通りある直線に平行な直線のベクトル方程式 | | 定点を通りある直線に平行な直線のベクトル方程式 |
| | | |
| 50行目: |
50行目: |
| <math>m (x - x_1 ) - l (y - y_1) = 0</math> | | <math>m (x - x_1 ) - l (y - y_1) = 0</math> |
| <br> | | <br> |
| | |
| ==== 異なる2点を通る直線のベクトル方程式(共線条件) ==== | | ==== 異なる2点を通る直線のベクトル方程式(共線条件) ==== |
| 異なる2点を通る直線のベクトル方程式(共線条件)の定義 | | 異なる2点を通る直線のベクトル方程式(共線条件)の定義 |
| 95行目: |
96行目: |
| 上記の連立方程式からtを消去すると、直線の式 <math>y = 2x - 3</math> が成り立つことがわかる。<br> | | 上記の連立方程式からtを消去すると、直線の式 <math>y = 2x - 3</math> が成り立つことがわかる。<br> |
| <br> | | <br> |
| ==== 定点 <math>A(\vec{a})</math> を通り、ベクトル <math>\vec{n}</math> に垂直な直線のベクトル方程式 ==== | | ==== 定点を通り、あるベクトルに垂直な直線のベクトル方程式 ==== |
| 定点を通り,ある直線に垂直な直線のベクトル方程式の定義 | | 定点を通り,ある直線に垂直な直線のベクトル方程式の定義 |
| | | |
| 203行目: |
204行目: |
| <br> | | <br> |
| ==== 平行四辺形OACB ==== | | ==== 平行四辺形OACB ==== |
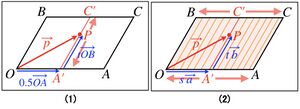
| | 例えば、<math>s = 0.5</math> の時、<math>\vec{p} = 0.5 \overrightarrow{OA} + t \overrightarrow{OB}</math> となり、<br> |
| | tを <math>0 \le t \le 1</math> の範囲で変化させる時、点Pは、下図(1)の線分OBに平行な線分A'C'上を動く。<br> |
| | [[ファイル:Vector Equation 6.jpg|フレームなし|中央]] |
| | <br> |
| | 次に、sを <math>0 \le s \le 1</math> の範囲で変化させる時、上図(2)のように、線分A'C'は、線分OBから線分ACまで平行に動く。<br> |
| | <br> |
| | したがって、<br> |
| | <math> |
| | \begin{cases} |
| | \vec{p} = s \vec{a} + t \vec{b} \\ |
| | 0 \le s \le 1 \\ |
| | 0 \le t \le 1 \\ |
| | \end{cases} |
| | \qquad |
| | \mbox{は 、 平 行 四 辺 形 OACB の 周 と 内 部 を 表 す } |
| | </math> |
| <br><br> | | <br><br> |
|
| |
|
| 214行目: |
231行目: |
| <math>(\vec{p} - \vec{c}) \cdot (\vec{p} - \vec{c}) = r^2</math> | | <math>(\vec{p} - \vec{c}) \cdot (\vec{p} - \vec{c}) = r^2</math> |
| <br> | | <br> |
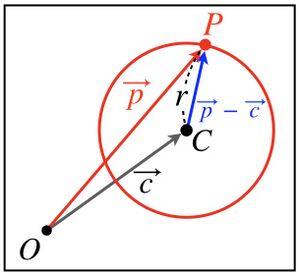
| 中心C、半径rの円上にある点Pについて考える。<br>
| | 下図に示すように、中心C、半径rの円上にある点Pについて考える。<br> |
| | [[ファイル:Vector Equation 9.jpg|フレームなし|中央]] |
| | <br> |
| 円の定義は、"中心Cからの距離がrである点の集まり"であるため、<math>CP = r</math> である。<br> | | 円の定義は、"中心Cからの距離がrである点の集まり"であるため、<math>CP = r</math> である。<br> |
| ベクトルで表すと、<math>| \overrightarrow{CP} | = r \quad \mbox{よ り } \quad | \vec{p} - \vec{c} | = r</math> である。<br> | | ベクトルで表すと、<math>| \overrightarrow{CP} | = r \quad \mbox{よ り } \quad | \vec{p} - \vec{c} | = r</math> である。<br> |
| 222行目: |
241行目: |
| <br> | | <br> |
| また、<math>C(a, b), \, P(x, y)</math> として成分で表すと、<math>(x - a)^2 + (y - b)^2 = r^2</math> であり、円の方程式となる。<br> | | また、<math>C(a, b), \, P(x, y)</math> として成分で表すと、<math>(x - a)^2 + (y - b)^2 = r^2</math> であり、円の方程式となる。<br> |
| | <br> |
| | * 例. 点C(3, 2)が中心で、点R(1, 1)が通る円 |
| | P(x, y)、O(0, 0)、C(3, 2)、R(1, 1)とする。<br> |
| | <math>| \overrightarrow{CP} | = | \overrightarrow{CR} |</math><br> |
| | <math>| \overrightarrow{OP} - \overrightarrow{OC} | = | \overrightarrow{OR} - \overrightarrow{OC} |</math><br> |
| | <br> |
| | <math>OP = (x, y), \, OC = (3, 2), \, OR = (1, 1)</math> より、<br> |
| | <math>| (x - 3, y - 2) | = | (-2, -1) |</math><br> |
| | <math>\sqrt{(x - 3)^2 + (y - 2)^2} = \sqrt{5}</math><br> |
| | <math>(x - 3)^2 + (y - 2)^2 = 5</math><br> |
| | <br> |
| | したがって、円の方程式は、<math>(x - 3)^2 + (y - 2)^2 = 5</math> となる。<br> |
| | <br> |
| | |
| | ==== 直径がABの円のベクトル方程式 ==== |
| | 円のベクトル方程式の定義 2 |
| | |
| | 3つの定点を <math>A(\vec{a}), \, B(\vec{b})</math> 、円周上の任意の点を <math>P(\vec{p})</math> とする。 |
| | <math>(\vec{p} - \vec{a}) \cdot (\vec{p} - \vec{b}) = 0</math> |
| | <br> |
| | 下図に示すように、直径がABの円周上の点Pについて考える。<br> |
| | [[ファイル:Vector Equation 10.jpg|フレームなし|中央]] |
| | <br> |
| | 直径に対する円周角は直角であるから、<math>AP \perp BP</math> であり、 <math>\overrightarrow{AP} \cdot \overrightarrow{BP} = 0</math> となる。<br> |
| | したがって、次式となる。<br> |
| | <math>(\overrightarrow{OP} - \overrightarrow{OA}) \cdot (\overrightarrow{OP} - \overrightarrow{OB}) = 0</math><br> |
| | <math>\therefore (\vec{p} - \vec{a}) \cdot (\vec{p} - \vec{b}) = 0</math><br> |
| | <br> |
| | * 例1. 円の中心がC(3. 2)で、点R(1, 1)を通る円 |
| | *: 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、 |
| | *: <math>| \overrightarrow{CP} | = | \overrightarrow{CR} |</math> |
| | *: <math>| \overrightarrow{OP} - \overrightarrow{OC} | = | \overrightarrow{OR} - \overrightarrow{OC} |</math> |
| | *: <br> |
| | *: <math>\overrightarrow{OP} = (x, y), \, \overrightarrow{OC} = (3 , 2), \, \overrightarrow{OR} = (1, 1)</math> より、 |
| | *: <math>| (x - 3, y - 2) | = | (-2, -1) |</math> |
| | *: <math>\sqrt{(x - 3)^2 + (y - 2)^2} = \sqrt{5}</math> |
| | *: <math>(x - 3)^2 + (y - 2)^2 = 5</math> |
| | *: <br> |
| | *: したがって、<math>(x - 3)^2 + (y - 2)^2 = 5</math> となる。 |
| | *: <br> |
| | * 例2. 点A(2, 5)と点B(4, 1)を直径の両端とする円 |
| | *: 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、 |
| | *: <math>\overrightarrow{AP} \cdot \overrightarrow{BP} = 0 \qquad \because \overrightarrow{AP} \bot \overrightarrow{BP}</math> |
| | *: <math>(\overrightarrow{OP} - \overrightarrow{OA}) \cdot (\overrightarrow{OP} - \overrightarrow{OB}) = 0</math> |
| | *: <br> |
| | *: <math>\overrightarrow{OP} = (x, y), \, \overrightarrow{OA} = (2 , 5), \, \overrightarrow{OB} = (4, 1)</math> より、 |
| | *: <math>(x - 2, y - 5) \cdot (x - 4, y - 1) = 0</math> |
| | *: <math>x^2 - 6x + y^2 - 6y + 13 = 0</math> |
| | *: <math>(x - 3)^2 - 9 + (y - 3)^2 - 9 = -13</math> |
| | *: <math>(x - 3)^2 + (y - 3)^2 = 5</math> |
| | *: <br> |
| | *: したがって、<math>(x - 3)^2 + (y - 3)^2 = 5</math> となる。 |
| | <br> |
| | |
| | ==== 円の接線のベクトル方程式 ==== |
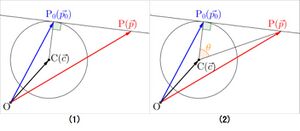
| | 下図(1)のように、円の中心点 <math>C(\vec{c})</math>、円周上の接点を <math>P_0(\vec{p_0})</math> とする時、接線上の点 <math>P(\vec{p})</math> の位置ベクトルは、次式となる。<br> |
| | [[ファイル:Vector Equation 11.jpg|フレームなし|中央]] |
| | <br> |
| | <math>\overrightarrow{P_0 P} \cdot \overrightarrow{CP_0} = 0</math><br> |
| | <math>( \overrightarrow{p} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> |
| | <br> |
| | また、下図(2)より、<math>| \overrightarrow{CP} | \cos{\theta} = | \overrightarrow{CP_0} |</math><br> |
| | <br> |
| | 両辺に、<math>| \overrightarrow{CP_0} |</math> を乗算すると、<br> |
| | <math>| \overrightarrow{CP} | | \overrightarrow{CP_0} | \cos{\theta} = | \overrightarrow{CP_0} |^2</math><br> |
| | <math>\overrightarrow{CP} \cdot \overrightarrow{CP_0} = r^2</math><br> |
| | <br> |
| | したがって、<math>( \overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = r^2 \qquad (1)</math> となる。<br> |
| | <br> |
| | (1)式は、次のようにしても求めることができる。<br> |
| | <math>( \overrightarrow{p} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> |
| | <math>( \overrightarrow{p} - \overrightarrow{c} + \overrightarrow{c} - \overrightarrow{p_0} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) = 0</math><br> |
| | これを展開する。<br> |
| | <math> |
| | \begin{align} |
| | (\overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) &= ( \overrightarrow{p_0} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) \\ |
| | &= | \overrightarrow{p_0} - \overrightarrow{c} |^2 \\ |
| | &= r^2 |
| | \end{align} |
| | </math><br> |
| | <br> |
| | 点Pの位置ベクトルを <math>P(\vec{p}) = (x, y)</math>、円の中心Cの位置ベクトル <math>C(\vec{c}) = (a, b)</math>、接点P<sub>0</sub>の位置ベクトル <math>P_0(\vec{p_0}) = (x_0, y_0)</math> とする。<br> |
| | <math>( \overrightarrow{p} - \overrightarrow{c} ) \cdot ( \overrightarrow{p_0} - \overrightarrow{c} ) =r^2</math><br> |
| | <math>(x - a, y - b) \cdot (x_0 - a, y_0 - b) = r^2</math><br> |
| | <math>(x_0 - a)(x - a) + (y_0 - b)(y - b) = r^2</math><br> |
| | <br> |
| | これは、円の接線の方程式を表していることが分かる。<br> |
| | <br> |
| | * 例. 円の中心 <math>C(1, 1)</math>、半径 <math>\sqrt{2}</math> の円に、<math>P(2, 2)</math> で接する接線の方程式をベクトルを用いて求めよ。 |
| | *: <math>\overrightarrow{OC} = (1, 1), \, \overrightarrow{OA} = (2, 2), \, \overrightarrow{OP} = (x, y)</math> とする。 |
| | *: <math>\overrightarrow{AP} \cdot \overrightarrow{AC} = 0 \quad \Longrightarrow \quad (\vec{p} - \vec{a}) \cdot (\vec{c} - \vec{a}) = 0</math> より、 |
| | *: <math>(x - 2, y - 2) \cdot (1, 1) = x - 2 + y - 2 = x - y - 4 = 0</math> |
| | *: <math>\therefore y = -x + 4</math> |
| <br><br> | | <br><br> |
|
| |
|
| __FORCETOC__ | | __FORCETOC__ |
| [[カテゴリ:解析学]] | | [[カテゴリ:解析学]] |
概要
ベクトル方程式とは、"ある条件を満たす点を、ベクトルで表現した式"のことである。
直線は、点の集合である。
例えば,直線  は、点(x, y)が満たす条件を式にしたもので,この条件を満たす点の集合が直線になる。
は、点(x, y)が満たす条件を式にしたもので,この条件を満たす点の集合が直線になる。
ベクトルでは、点の位置を表すために、位置ベクトルが存在する。
この位置ベクトルを利用して、曲線上の点の位置ベクトル  の満たす関係式を、その曲線のベクトル方程式という。
の満たす関係式を、その曲線のベクトル方程式という。
直線のベクトル方程式
定点を通り、ある直線に平行な直線のベクトル方程式
定点を通りある直線に平行な直線のベクトル方程式
定点  を通り、
を通り、 でないベクトル
でないベクトル  に平行な直線のベクトル方程式
に平行な直線のベクトル方程式

点  を通り、
を通り、 でないベクトル
でないベクトル  に平行な直線をgとする。
に平行な直線をgとする。
点  が直線g上にあるということは、
が直線g上にあるということは、 と表すことができる。
と表すことができる。
 より、
より、


と表すことができる。
この時、 を直線gの方向ベクトルtを媒介変数という。
を直線gの方向ベクトルtを媒介変数という。
また、このベクトル方程式をベクトルの成分で表すことを考える。
原点をO、点Aの座標を  、直線g上の任意の点を
、直線g上の任意の点を  として、
として、 とする時、
とする時、
ベクトル方程式は、次式となる。


媒介変数tを用いて表されたこの連立方程式を、直線gの媒介変数表示という。
この連立方程式からtを消去する時、次のことが成り立つ。
点  を通り、
を通り、 が方向ベクトルである直線の方程式
が方向ベクトルである直線の方程式

異なる2点を通る直線のベクトル方程式(共線条件)
異なる2点を通る直線のベクトル方程式(共線条件)の定義
異なる2点  を通る直線のベクトル方程式は、次式となる。
を通る直線のベクトル方程式は、次式となる。
 または
または

平面上の異なる2点  を通る直線上に,点
を通る直線上に,点  があることを考える。
があることを考える。
この時、 と表されるので、次式となる。
と表されるので、次式となる。

上式の方程式において、 とおく時、次式としても表すことができる。
とおく時、次式としても表すことができる。

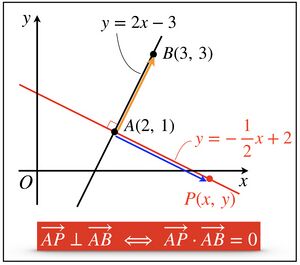
例.  の時、直線ABの式は
の時、直線ABの式は  である。
である。
P(x, y)として、ベクトルで考えると

したがって、次式のように媒介変数表示で表すことができる。

上記の連立方程式からtを消去すると、直線の式  が成り立つことがわかる。
が成り立つことがわかる。
定点を通り、あるベクトルに垂直な直線のベクトル方程式
定点を通り,ある直線に垂直な直線のベクトル方程式の定義
定点  を通り、
を通り、 でないベクトル
でないベクトル  に垂直な直線のベクトル方程式
に垂直な直線のベクトル方程式
 (
( は直線の法線ベクトル)
は直線の法線ベクトル)
下図に、定点  を通り、ベクトル
を通り、ベクトル  に垂直な直線を示す。
に垂直な直線を示す。
点  がこの直線上にあるということは、
がこの直線上にあるということは、 である。
である。
内積を用いて表すと、次式となる。


例. 点  、直線ABの式
、直線ABの式  とする時、この直線に垂直な直線の式を求める。
とする時、この直線に垂直な直線の式を求める。
P(x, y) として、ベクトルで考える。





したがって、ベクトル方程式  を用いて、定点
を用いて、定点  を通り、ベクトル
を通り、ベクトル  に垂直な直線を表すことができる。
に垂直な直線を表すことができる。
ベクトルの終点の存在範囲
定義
ベクトルの終点の存在範囲の定義
 とする。(s、tは実数の変数)
s、tに条件がある時,次のような図形を表す。
直線AB
とする。(s、tは実数の変数)
s、tに条件がある時,次のような図形を表す。
直線AB
 線分AB
線分AB

 の周と内部
の周と内部
 平行四辺形OACBの周と内部
平行四辺形OACBの周と内部

直線AB
異なる2点を通る直線のベクトル方程式の通り、点  が次式を満たしながら動く時、点
が次式を満たしながら動く時、点  の存在範囲は直線ABとなる。
の存在範囲は直線ABとなる。

線分AB
点  の存在範囲を線分AB上に限定する場合を考える。
の存在範囲を線分AB上に限定する場合を考える。
 の時、点
の時、点  は、点
は、点  と一致する。
と一致する。 の時、点
の時、点  は、線分ABの中点に位置する。
は、線分ABの中点に位置する。 の時、点
の時、点  は、点
は、点  と一致する。
と一致する。
つまり、 の時、線分ABを表現することができる。
の時、線分ABを表現することができる。

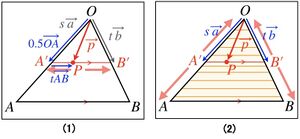
△OAB
例えば、 の時、次式となり、
の時、次式となり、
tを  の範囲で変化させると、点Pは、下図(1)のように、線分ABに平行な線分A'B'上を動く。
の範囲で変化させると、点Pは、下図(1)のように、線分ABに平行な線分A'B'上を動く。

そして、 を、
を、 の範囲で変化させると、線分A'B'は、上図(2)のように、△OABの全体を動く。
の範囲で変化させると、線分A'B'は、上図(2)のように、△OABの全体を動く。
したがって、

平行四辺形OACB
例えば、 の時、
の時、 となり、
となり、
tを  の範囲で変化させる時、点Pは、下図(1)の線分OBに平行な線分A'C'上を動く。
の範囲で変化させる時、点Pは、下図(1)の線分OBに平行な線分A'C'上を動く。
次に、sを  の範囲で変化させる時、上図(2)のように、線分A'C'は、線分OBから線分ACまで平行に動く。
の範囲で変化させる時、上図(2)のように、線分A'C'は、線分OBから線分ACまで平行に動く。
したがって、

円のベクトル方程式
中心がC,半径がrの円のベクトル方程式
中心がC、半径がrの円のベクトル方程式の定義
3つの定点を  、円周上の任意の点を
、円周上の任意の点を  とする。
とする。
 または
または

下図に示すように、中心C、半径rの円上にある点Pについて考える。
円の定義は、"中心Cからの距離がrである点の集まり"であるため、 である。
である。
ベクトルで表すと、 である。
である。
ゆえに、
したがって、
また、 として成分で表すと、
として成分で表すと、 であり、円の方程式となる。
であり、円の方程式となる。
- 例. 点C(3, 2)が中心で、点R(1, 1)が通る円
P(x, y)、O(0, 0)、C(3, 2)、R(1, 1)とする。


 より、
より、



したがって、円の方程式は、 となる。
となる。
直径がABの円のベクトル方程式
円のベクトル方程式の定義 2
3つの定点を  、円周上の任意の点を
、円周上の任意の点を  とする。
とする。

下図に示すように、直径がABの円周上の点Pについて考える。
直径に対する円周角は直角であるから、 であり、
であり、  となる。
となる。
したがって、次式となる。


- 例1. 円の中心がC(3. 2)で、点R(1, 1)を通る円
- 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、


 より、
より、


- したがって、
 となる。
となる。
- 例2. 点A(2, 5)と点B(4, 1)を直径の両端とする円
- 円周上の点Rから円の中心Cを通る直線PRがあり、その円周上の点をP(x, y)とする時、


 より、
より、



- したがって、
 となる。
となる。
円の接線のベクトル方程式
下図(1)のように、円の中心点  、円周上の接点を
、円周上の接点を  とする時、接線上の点
とする時、接線上の点  の位置ベクトルは、次式となる。
の位置ベクトルは、次式となる。


また、下図(2)より、
両辺に、 を乗算すると、
を乗算すると、


したがって、 となる。
となる。
(1)式は、次のようにしても求めることができる。


これを展開する。

点Pの位置ベクトルを  、円の中心Cの位置ベクトル
、円の中心Cの位置ベクトル  、接点P0の位置ベクトル
、接点P0の位置ベクトル  とする。
とする。



これは、円の接線の方程式を表していることが分かる。
- 例. 円の中心
 、半径
、半径  の円に、
の円に、 で接する接線の方程式をベクトルを用いて求めよ。
で接する接線の方程式をベクトルを用いて求めよ。
 とする。
とする。 より、
より、