応用数学 - 広義積分と無限積分

概要

広義積分および無限積分について理解する。

極限の例題

例題:
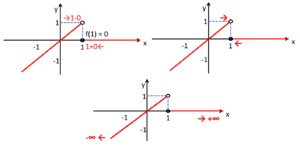
$f(x)={\begin{cases}x&\qquad (x<1)\\0&\qquad (x\geq 1)\end{cases}}$
について、以下の極限を求めよ。

(1) $\lim _{x\to 1+0}{f(x)}$
(2) $\lim _{x\to 1-0}{f(x)}$
(3) $\lim _{x\to 1}{f(x)}$
(4) $\lim _{x\to +\infty }{f(x)}$
(5) $\lim _{x\to -\infty }{f(x)}$

解答:
(1)
xを正の方向から1に近づけた極限なので、
$\lim _{x\to 1+0}{f(x)}=0$

(2)
xを負の方向から1に近づけた極限なので、
$\lim _{x\to 1-0}{f(x)}=1$

(3)
xを正と負の両方から近づけた極限である。
しかし、(1)(2)より、右側極限と左側極限は一致しない。
そのため、一定の値には収束しないので、
$\lim _{x\to 1}{f(x)}$ は値なし。

(4)
xを限りなく大きくしたときの極限なので、
$\lim _{x\to +\infty }{f(x)}=0\qquad ({\mbox{ 収 束 }})$

(5)
xを限りなく小さくしたときの極限なので、
$\lim _{x\to -\infty }{f(x)}=-\infty \qquad ({\mbox{ 発 散 }})$

連続な関数

定義:
関数 $f(x)$ が $x=a$ で連続とは、以下の条件を満たすことである。
(1) $f(a)$ が存在する。
(2) $\lim _{x\to a}{f(x)}$ が存在する。
(3) $\lim _{x\to a}{f(x)}=f(a)$

関数 $f(x)$ が区間Iで連続とは、以下の条件を満たすことである。
区間Iの任意の値aについて、$f(x)$ は $x=a$ で連続。

区分的に連続な関数

定義:
$a\leq x\leq b$ で定義された関数 $f(x)$ が以下の条件を満たすとき、 $f(x)$ は $a\leq x\leq b$ で区分的に連続(piecewisely continuous)であるという。

(1) $f(x)$ は $a\leq x\leq b$ において有限個の点を除いて連続である。
(2) $f(x)$ の不連続な点cにおいては、以下で示す右側極限と左側極限が存在する。
    $\lim _{x\to c+0}{f(x)}\qquad \lim _{x\to c-0}{f(x)}$

$f(x)$ が $a\leq x\leq b$ で区分的に連続であるとは、言い換えると以下の条件を満たすことである。
(1) 不連続な点があっても有限個である。
(2) 不連続な点では、値が $+\infty$ や $-\infty$ に発散したり振動したりしない。

このような区分的に連続な関数に対しては、連続な関数とほぼ同様に定積分を行うことができる。

下図に、区分的に連続な関数を示す。

図. $a\leq x\leq b$ において区分的に連続な関数 $f(x)$

ラプラス変換では、このような関数を扱う。