回路計算 - 合成インピーダンス

RL並列回路の合成インピーダンス

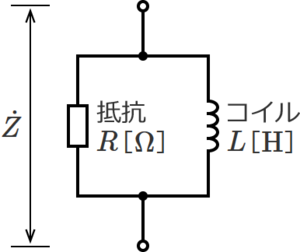
RL並列回路は、抵抗RとコイルLが並列に接続された回路で、下図のような回路になる。

図.1 抵抗RとコイルLが並列接続の回路

並列回路の合成インピーダンス${\dot {Z}}$を求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。

RL並列回路の合成インピーダンス${\dot {Z}}$は、次式で与えられる。
なお、角周波数$\omega =2\pi f$である。

• 複素数表示の場合

${\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{R}}+{\frac {1}{j\omega L}}\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{R}}+{\frac {1}{j\omega L}}}}\\&={\frac {j\omega RL}{R+j\omega L}}\\&={\frac {j\omega RL(R-j\omega L)}{R^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}+j\omega R^{2}L}{R^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L}{R^{2}+(\omega L)^{2}}}\quad [\Omega ]\end{aligned}}$

$\omega \geq 0,\quad R>0,\quad L>0$であるため、
$\Re (Z)={\frac {\omega ^{2}RL^{2}}{R^{2}+(\omega L)^{2}}}>0,\quad \Im (Z)={\frac {\omega R^{2}L}{R^{2}+(\omega L)^{2}}}>0$となり、
RL並列回路の合成インピーダンス${\dot {Z}}$のベクトルの向きは、必ず右上向き(複素数平面の第1象限)になる。

• 合成インピーダンスの大きさの場合

${\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{R}}+{\frac {1}{j\omega L}}}}\\&={\frac {j\omega RL}{R+j\omega L}}\\\left|Z\right|&={\frac {\sqrt {(\omega RL)^{2}}}{\sqrt {R^{2}+(\omega L)^{2}}}}\\&={\frac {\omega RL}{\sqrt {R^{2}+(\omega L)^{2}}}}\quad [\Omega ]\end{aligned}}$

RC並列回路の合成インピーダンス

RC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。

図.2 抵抗RとコンデンサCが並列接続の回路

並列回路の合成インピーダンス${\dot {Z}}$を求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。

RC並列回路の合成インピーダンス${\dot {Z}}$は、次式で与えられる。
なお、角周波数$\omega =2\pi f$である。

• 複素数表示の場合

${\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{R}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{R}}+j\omega C}}\\&={\frac {R}{1+j\omega RC}}\\&={\frac {R(1-j\omega RC)}{1+(\omega RC)^{2}}}\\&={\frac {R-j\omega R^{2}C}{1+(\omega RC)^{2}}}\\&={\frac {R}{1+(\omega RC)^{2}}}-j{\frac {\omega R^{2}C}{1+(\omega RC)^{2}}}\quad [\Omega ]\end{aligned}}$

$\omega \geq 0,\quad R>0,\quad C>0$であるため、
$\Re (Z)={\frac {R}{1+(\omega RC)^{2}}}>0,\quad \Im (Z)={\frac {\omega R^{2}C}{1+(\omega RC)^{2}}}>0$となり、
RC並列回路の合成インピーダンス${\dot {Z}}$のベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。

• 合成インピーダンスの大きさの場合

${\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{R}}+j\omega C}}\\&={\frac {R}{1+j\omega RC}}\\\left|Z\right|&={\frac {\sqrt {R^{2}}}{\sqrt {1^{2}+(\omega RC)^{2}}}}\\&={\frac {R}{\sqrt {1+(\omega RC)^{2}}}}\quad [\Omega ]\end{aligned}}$

LC並列回路の合成インピーダンス

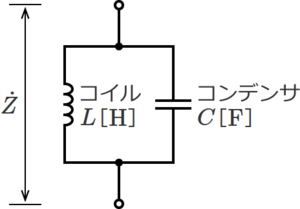
LC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。

図.3 コイルLとコンデンサCが並列接続の回路

並列回路の合成インピーダンス${\dot {Z}}$を求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。

LC並列回路の合成インピーダンス${\dot {Z}}$は、次式で与えられる。
なお、角周波数$\omega =2\pi f$である。

• 複素数表示の場合

${\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{j\omega L}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{j\omega L}}+j\omega C}}\\&=j{\frac {\omega L}{1-\omega ^{2}LC}}\quad [\Omega ]\end{aligned}}$

$\omega \geq 0,\quad L>0,\quad C>0$であるため、
$\Re (Z)=0,\quad -\infty <\Im (Z)={\frac {\omega L}{1-\omega ^{2}LC}}<\infty$となり、
LC並列回路の合成インピーダンス${\dot {Z}}$のベクトルの向きは、必ず、虚数軸上となる。

LC並列回路の合成インピーダンス${\dot {Z}}$は、上式の分母が正・負・ゼロの時、それぞれ${\dot {Z}}$のベクトルの向きが変わる。
したがって、$1-\omega ^{2}LC>0,\quad 1-\omega ^{2}LC<0,\quad 1-\omega ^{2}LC=0$の時で、場合分けして考える必要がある。

• $1-\omega ^{2}LC>0$の場合

  上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きになる。

  
  

• $1-\omega ^{2}LC<0$の場合

  上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、虚数軸上の負の向きになる。

  
  

• $1-\omega ^{2}LC=0$の場合

  上式のリアクタンスが無限大になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きに無限大となる。

  インピーダンスが無限大ということは、その回路は開放状態と同じになる。

  
  

  また、$1-\omega ^{2}LC=0$ すなわち、$\omega ={\frac {1}{\sqrt {LC}}}$ は、回路の共振条件である。

• 合成インピーダンスの大きさの場合

${\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{j\omega L}}+j\omega C}}\\&={\frac {j\omega L}{1-\omega ^{2}LC}}\\\left|Z\right|&={\frac {\sqrt {(\omega L)^{2}}}{\sqrt {1^{2}+(\omega ^{2}LC)^{2}}}}\\&=\left|{\frac {\omega L}{\sqrt {1+(\omega ^{2}LC)^{2}}}}\right|\quad [\Omega ]\end{aligned}}$

RLC並列回路の合成インピーダンス

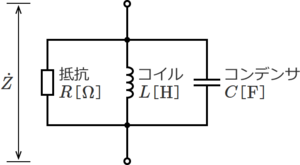
RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。

図.4 抵抗R、コイルL、コンデンサCが並列接続の回路

並列回路の合成インピーダンス${\dot {Z}}$を求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。

RLC並列回路の合成インピーダンス${\dot {Z}}$は、次式で与えられる。
なお、角周波数$\omega =2\pi f$である。

• 複素数表示の場合

${\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}+{\dot {Y_{3}}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}+{\dot {Y_{3}}}}}={\frac {j\omega RL}{R+j\omega L-\omega ^{2}RLC}}\\&={\frac {j\omega RL}{R-\omega ^{2}RLC+j\omega L}}\\&={\frac {j\omega RL(R-\omega ^{2}RLC-j\omega L)}{(R-\omega ^{2}RLC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}+j\omega R^{2}L-j\omega ^{3}R^{2}L^{2}C}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L-\omega ^{3}R^{2}L^{2}C}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L(1-\omega ^{2}LC)}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\quad [\Omega ]\end{aligned}}$

$\omega \geq 0,\quad R>0,\quad L>0$であるため、
$\Re (Z)={\frac {\omega ^{2}RL^{2}}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}>0,\quad -\infty <\Im (Z)={\frac {\omega R^{2}L(1-\omega ^{2}LC)}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}<\infty$となり、
RLC並列回路の合成インピーダンス${\dot {Z}}$のベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。

RLC並列回路の合成インピーダンス${\dot {Z}}$は、上式の分子(特に、$1-\omega ^{2}LC$)が正・負・ゼロの時、それぞれ${\dot {Z}}$のベクトルの向きが変わる。
したがって、$1-\omega ^{2}LC>0,\quad 1-\omega ^{2}LC<0,\quad 1-\omega ^{2}LC=0$の時で、場合分けして考える必要がある。

• $1-\omega ^{2}LC>0$の場合

  上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、右上の向き(第1象限)になる。

  
  

• $1-\omega ^{2}LC<0$の場合

  上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、右下の向き(第4象限)になる。

  
  

• $1-\omega ^{2}LC=0$の場合

  上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、実数軸上の正の向きになる。(${\dot {Z}}=R[\Omega ]$)

  この条件を満たす周波数は反共振周波数であるため、コイルLとコンデンサCの並列回路部分は開放状態と同じになる。

  
  

  また、$1-\omega ^{2}LC=0$ すなわち、$\omega ={\frac {1}{\sqrt {LC}}}$ は、回路の共振条件である。

• 合成インピーダンスの大きさの場合

${\begin{aligned}{\dot {Z}}&={\frac {j\omega RL}{R+j\omega L-\omega ^{2}RLC}}\\&={\frac {j\omega RL}{R-\omega ^{2}RLC+j\omega L}}\\&={\frac {j\omega RL}{R(1-\omega ^{2}LC)+j\omega L}}\\\left|Z\right|&={\frac {\sqrt {(\omega RL)^{2}}}{\sqrt {R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}}\\&={\frac {\omega RL}{\sqrt {R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}}\quad [\Omega ]\end{aligned}}$