「第7回 - ベイズの定理」の版間の差分
| (同じ利用者による、間の2版が非表示) | |||
| 44行目: | 44行目: | ||
<br> | <br> | ||
さらに、上式をまとめると次式となる。<br> | さらに、上式をまとめると次式となる。<br> | ||
<math> | |||
\begin{align} | |||
P(A|B) \times P(B) &= P(B|A) \times P(A) \mbox{ よ り }\\ | |||
P(A|B) &= \frac{P(B|A) \times P(A)}{P(B)} | |||
\end{align} | |||
</math><br> | |||
<br> | <br> | ||
<math>P(A | あるいは下図に示すように、事象Aが起こるという条件のもとで、K種類の事象(これらは互いに排反とする)が起きる時、<br> | ||
事象Aが起きるという条件のもとで、事象B<sub>i</sub>が起きる条件付き確率は、次式から求められる。<br> | |||
<math>P(B_{i}|A) = \frac{P(A \cap B_{i})}{P(A)} = \frac{P(A|B_{i}) \times P(B_{i})}{P(A)}</math><br> | |||
<br> | <br> | ||
<math>P(A| | また、<math>P(A) = P(A \cap B_{1}) + P(A \cap B_{2}) \cdots + P(A \cap B_{K})</math>である。<br> | ||
これは、上図のそれぞれの事象における赤い事象Aの部分を足し合わせたものだと考えることができる。<br> | |||
<math> | |||
\begin{align} | |||
P(B_{i}|A) &= \frac{P(A|B_{i}) \times P(B_{i})}{P(A)}\\ | |||
&= \frac{P(A|B_{i}) \times P(B_{i})}{P(A \cap B_{1}) + P(A \cap B_{2}) \cdots + P(A \cap B_{K})} \\ | |||
&= \frac{P(A|B_{i}) \times P(B_{i})}{\sum_{i=1}^K P(B_{i}) P(A|B_{i})} | |||
\end{align} | |||
</math><br> | |||
[[ファイル:Statistics 7 1.png|フレームなし|中央]] | |||
<br> | <br> | ||
ベイズの定理とは、先に事象Bが起きた場合に、後の事象Aが起きる場合の確率P(A|B)が分かっている場合において、<br> | |||
逆に後の事象Aが起きたと分かっている時に、先の事象Bが起きる場合の確率P(B|A)を与えるものである。<br> | 逆に後の事象Aが起きたと分かっている時に、先の事象Bが起きる場合の確率P(B|A)を与えるものである。<br> | ||
<br><br> | <br><br> | ||
| 76行目: | 90行目: | ||
検査装置が"検出した"事象には、"本当にガン"場合と"ガンでない"場合の両方が含まれる。<br> | 検査装置が"検出した"事象には、"本当にガン"場合と"ガンでない"場合の両方が含まれる。<br> | ||
そのため、"検出した"事象(下図の赤枠)を全体事象とみなす時、"本当に癌である"である確率を求める。<br> | そのため、"検出した"事象(下図の赤枠)を全体事象とみなす時、"本当に癌である"である確率を求める。<br> | ||
[[ファイル:Statistics 7 2.png|フレームなし|中央]] | |||
<br> | <br> | ||
以下に、求める手順を示す。<br> | 以下に、求める手順を示す。<br> | ||
2021年8月9日 (月) 02:13時点における最新版
概要
推定統計を学習する準備として、確率の基礎に関する次の事項を記載する。
- 条件付き確率
- ベイズの定理
条件付き確率
条件付き確率とは、2個の事象AとBがあるとき、既に事象Aが起きた場合に、事象Bも合わせて起きる確率を条件付き確率P(B|A)という。
P(B|A)
P(左 : 合わせて起きる事象 | 右 : 既に起きた事象)
条件付き確率の式(事象Aが起きた場合に、事象Bも合わせて起きる条件付き確率)は、次式で表される。
条件付き確率P(B|A)と同時確率P(A∩B)の違い
- 条件付き確率P(B|A)
- 全事象をAのみとしている。
- つまり、事象Aが起きた場合の中で、さらに事象Bも起きる確率P(B|A)を考える。
- 同時確率P(A∩B)
- 全事象をUとしている。
- つまり、事象Aが起きた場合のみに限定せず、A以外が起きる場合も合わせた上で事象AとBが同時に起きる確率を考える。
ベイズの定理
以下に、ベイズの定理の導出過程を示す。
条件付き確率の計算式の2式
上式より、次式が求まる。
さらに、上式をまとめると次式となる。
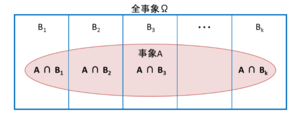
あるいは下図に示すように、事象Aが起こるという条件のもとで、K種類の事象(これらは互いに排反とする)が起きる時、
事象Aが起きるという条件のもとで、事象Biが起きる条件付き確率は、次式から求められる。
また、である。
これは、上図のそれぞれの事象における赤い事象Aの部分を足し合わせたものだと考えることができる。
ベイズの定理とは、先に事象Bが起きた場合に、後の事象Aが起きる場合の確率P(A|B)が分かっている場合において、
逆に後の事象Aが起きたと分かっている時に、先の事象Bが起きる場合の確率P(B|A)を与えるものである。
ベイズの定理の例
あるガンの検査装置の性能が以下の通りとする。
ここで、検出したを、癌であるを、癌ではないをとする。
- 癌である被験者を検査して、癌と検出した確率
- P(検出した | 癌である) = 0.9
- 癌ではない被験者を検査して、癌と検出した確率
- P(検出した | 癌ではない) = 0.1
- 癌である確率
- P(癌である) = 0.001
- 癌ではない確率
- P(癌ではない) = 0.999
この時、検査装置が検出した時に被験者が癌である確率P(ガンである|検出した)を求めよ。
検査装置が"検出した"事象には、"本当にガン"場合と"ガンでない"場合の両方が含まれる。
そのため、"検出した"事象(下図の赤枠)を全体事象とみなす時、"本当に癌である"である確率を求める。
以下に、求める手順を示す。
- "検出した、かつ、癌である" の確率を求める。
- P(検出した ∩ 癌である) = P(検出した | 癌である) × P(癌である)
- "検出した"事象(上図の赤枠)の範囲の確率を求める。
- P(検出した)
- P(癌である | 検出した)を求める。
- P(癌である | 検出した) = P(検出した ∩ 癌である) / P(検出した)
ベイズの定理より、下式を求める。
P(癌である | 検出した) = P(検出した | 癌である) × P(癌である) / P(検出した)
まず、P(検出した ∩ 癌である)を求める。
次に、P(検出した)の確率の値は無いため、和事象の確率の公式を用いて求める。
P(検出した) = P(検出した ∩ 癌である) + P(検出した ∩ 癌ではない)
= P(検出した | 癌である) × P(癌である) + P(検出した | 癌ではない) × P(癌ではない)
最後に、P(癌である | 検出した)の確率を求める。
したがって、検査装置の検査結果が癌と検出した場合であっても、実際に癌である確率は、P(癌である | 検出した) ≅ 0.00893しかない。
では、P(癌である | 検出した)の確率が十分に高くするには、検査装置の性能はどうあればよいかを考える。(例 : 0.9)
例えば、P(検出した | 癌である) = 0.9999、P(検出した | 癌ではない) = 0.0001とする時、以下の値となる。
したがって、P(癌である) = 0.001のような癌に罹る確率が低い時は、癌患者に対する検査装置の結果が癌と検出する確率は、
P(検出した | 癌である) = 0.9999と非常に高い確率でなくてはならない。