|
|
| (同じ利用者による、間の10版が非表示) |
| 59行目: |
59行目: |
| <math>f(t) = \frac{1}{2 \pi i} \int^{p + i \infty}_{p - i \infty} {e^{st} F(s) ds}</math> | | <math>f(t) = \frac{1}{2 \pi i} \int^{p + i \infty}_{p - i \infty} {e^{st} F(s) ds}</math> |
| | | |
| ここで、<math>s = p + i \alpha \quad (p, \, \alpha : \mbox{ 実 数 }, \, \, i : \mbox{ 虚 数 単 位 })</math> とする。 | | ここで、<math>s = p + i \alpha \quad (p, \, \alpha : \mbox{ 実 数 } \, , \, \, i : \mbox{ 虚 数 単 位 } \, )</math> とする。 |
| | | |
| 説明: | | 説明: |
| 70行目: |
70行目: |
| <math>f(t) = \frac{1}{2 \pi i} \int^{p + i \infty}_{p - i \infty} {e^{st} F(s) \, ds}</math> | | <math>f(t) = \frac{1}{2 \pi i} \int^{p + i \infty}_{p - i \infty} {e^{st} F(s) \, ds}</math> |
| | | |
| <math> \qquad s = p + i \alpha \quad (p, \, \alpha : \mbox{ 実 数 }, \, \, i : \mbox{ 虚 数 単 位 })</math><br> | | <math> \qquad s = p + i \alpha \quad (p, \, \alpha : \mbox{ 実 数 } \, , \, \, i : \mbox{ 虚 数 単 位 } \,)</math><br> |
| <br> | | <br> |
| 下図に、ブロムウィチ積分の積分経路を示す。<br> | | 下図に、ブロムウィチ積分の積分経路を示す。<br> |
| 98行目: |
98行目: |
| {| class="wikitable" | style="background-color:#fefefe;text-align: center;" | | {| class="wikitable" | style="background-color:#fefefe;text-align: center;" |
| |- | | |- |
| ! style="background-color:#66CCFF;width:30%" | <math>\definecolor{orgblack}{RGB}{20,20,20}\color{orgblack} f(t)</math> | | ! style="background-color:#66CCFF;width:30%" | <math>f(t)</math> |
| ! style="background-color:#66CCFF;width:30%" | <math>\definecolor{orgblack}{RGB}{20,20,20}\color{orgblack} F(s)</math> | | ! style="background-color:#66CCFF;width:30%" | <math>F(s)</math> |
| ! style="background-color:#66CCFF;width:40%" | 条件 | | ! style="background-color:#66CCFF;width:40%" | 条件 |
| |- | | |- |
| | <math>\color{Black} 1</math> || <math>\color{Black} \frac{1}{s}</math> || <math>\color{Black} s > 0</math> | | | <math>1</math> || <math>\frac{1}{s}</math> || <math>s > 0</math> |
| |- | | |- |
| | <math>\color{Black} t</math> || <math>\color{Black} \frac{1}{s^2}</math> || <math>\color{Black} s > 0</math> | | | <math>t</math> || <math>\frac{1}{s^2}</math> || <math>s > 0</math> |
| |- | | |- |
| | <math>\color{Black} \frac{t^{n - 1}}{(n - 1)!}</math> || <math>\color{Black} \frac{1}{s^{n}}</math> || <math>\color{Black} n</math> は正整数 | | | <math>\frac{t^{n - 1}}{(n - 1)!}</math> || <math>\frac{1}{s^{n}}</math> || <math>n</math> は正整数 |
| |- | | |- |
| | <math>\color{Black} \frac{t^{p - 1}}{\Gamma(p)}</math> || <math>\color{Black} \frac{1}{s^{p}}</math> || <math>\color{Black} p > 0</math> | | | <math>\frac{t^{p - 1}}{\Gamma(p)}</math> || <math>\frac{1}{s^{p}}</math> || <math>p > 0</math> |
| |- | | |- |
| | <math>\color{Black} e^{at}</math> || <math>\color{Black} \frac{1}{s - a}</math> || <math>\color{Black} s > \alpha</math> | | | <math>e^{at}</math> || <math>\frac{1}{s - a}</math> || <math>s > \alpha</math> |
| |- | | |- |
| | <math>\color{Black} \sin{at}</math> || <math>\color{Black} \frac{a}{s^2 + a^2}</math> || <math>\color{Black} s > 0, \quad a : \mbox{ 実 定 数 }</math> | | | <math>\sin{at}</math> || <math>\frac{a}{s^2 + a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 } \, \,</math> |
| |- | | |- |
| | <math>\cos{at}</math> || <math>\frac{s}{s^2 + a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 }</math> | | | <math>\cos{at}</math> || <math>\frac{s}{s^2 + a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 } \, \,</math> |
| |- | | |- |
| | <math>\sinh{at}</math> || <math>\frac{a}{s^2 - a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 }</math> | | | <math>\sinh{at}</math> || <math>\frac{a}{s^2 - a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 } \, \,</math> |
| |- | | |- |
| | <math>\cosh{at}</math> || <math>\frac{s}{s^2 - a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 }</math> | | | <math>\cosh{at}</math> || <math>\frac{s}{s^2 - a^2}</math> || <math>s > 0, \quad a : \mbox{ 実 定 数 } \, \,</math> |
| |- | | |- |
| | 単位階段関数 <math>U(t - a)</math> || <math>\frac{e^{-as}}{s}</math> || <math>s > 0, \quad a > 0</math> | | | 単位階段関数 <math>U(t - a)</math> || <math>\frac{e^{-as}}{s}</math> || <math>s > 0, \quad a > 0</math> |
| 146行目: |
146行目: |
| | 積分法則<br><math>\int^{t}_{0} {f(u) \, du}</math> || <math>\frac{F(s)}{s}</math> || | | | 積分法則<br><math>\int^{t}_{0} {f(u) \, du}</math> || <math>\frac{F(s)}{s}</math> || |
| |- | | |- |
| | <math>t^{n}</math> 積法則<br><math>t^{n} f(t)</math> || <math>(-1)^{n} \, \frac{dF^{n} (s)}{ds}</math> || <math>n : \mbox{ 正 整 数 }</math> | | | <math>t^{n}</math> 積法則<br><math>t^{n} f(t)</math> || <math>(-1)^{n} \, \frac{dF^{n} (s)}{ds^{n}}</math> || <math>n : \mbox{ 正 整 数 } \, \,</math> |
| |- | | |- |
| | 合成積<br><math>(f * g)(t)</math> || <math>F(s) \, G(s)</math> || | | | 合成積<br><math>(f * g)(t)</math> || <math>F(s) \, G(s)</math> || |
| 189行目: |
189行目: |
| *: <math>\frac{P(s)}{(s - a)^{3} (s^{2} + bs + c)} = \frac{A}{s - a} + \frac{B}{(s - a)^{2}} + \frac{C}{(s - a)^{3}} + \frac{Ds + E}{s^{2} + bs + c}</math> | | *: <math>\frac{P(s)}{(s - a)^{3} (s^{2} + bs + c)} = \frac{A}{s - a} + \frac{B}{(s - a)^{2}} + \frac{C}{(s - a)^{3}} + \frac{Ds + E}{s^{2} + bs + c}</math> |
| <br> | | <br> |
| 例題: | | 例題 1: |
| 部分分数展開とラプラス逆変換公式を使用することにより、以下のラプラス逆変換の値を求めよ。 | | 部分分数展開とラプラス逆変換公式を使用することにより、以下のラプラス逆変換の値を求めよ。 |
| <math>\mathcal{L}^{-1} \bigg[ \frac{s}{s^{2} - 4s + 3} \bigg]</math> | | <math>\mathcal{L}^{-1} \bigg[ \frac{s}{s^{2} - 4s + 3} \bigg]</math> |
| 212行目: |
212行目: |
| <math> | | <math> |
| \begin{align} | | \begin{align} |
| \mathcal{L}^{-1} \left[ \frac{s}{s^{2} - 4s + 3} \right] &= \mathcal{L}^{-1} \left[ \frac{3}{2} \frac{1}{s - 3} - \frac{1}{2} \frac{1}{s - 1} \right] \qquad \mbox{ 上 式 (2) }\\ | | \mathcal{L}^{-1} \left[ \frac{s}{s^{2} - 4s + 3} \right] &= \mathcal{L}^{-1} \left[ \frac{3}{2} \frac{1}{s - 3} - \frac{1}{2} \frac{1}{s - 1} \right] \qquad \mbox{ 上 式 (2) }\\ |
| &= \frac{3}{2} \, \mathcal{L}^{-1} \left[ \frac{1}{s - 3} \right] - \frac{1}{2} \, \mathcal{L}^{-1} \left[ \frac{1}{s - 1} \right] \qquad \because \mbox{ 線 形 法 則 } \\ | | &= \frac{3}{2} \, \mathcal{L}^{-1} \left[ \frac{1}{s - 3} \right] - \frac{1}{2} \, \mathcal{L}^{-1} \left[ \frac{1}{s - 1} \right] \qquad \because \mbox{ 線 形 法 則 } \\ |
| &= \frac{3}{2} e^{3t} - \frac{1}{2} e^{t} \qquad \because \mbox{ 変 換 公 式 } \\ | | &= \frac{3}{2} e^{3t} - \frac{1}{2} e^{t} \qquad \because \mbox{ 変 換 公 式 } \\ |
| &= \frac{3 e^{3t}}{2} - \frac{e^{t}}{2} | | &= \frac{3 e^{3t}}{2} - \frac{e^{t}}{2} |
| | \end{align} |
| | </math> |
| | <br> |
| | 例題 2: |
| | ラプラス変換を用いて、以下の初期値問題を求めよ。 |
| | <math> |
| | \begin{cases} |
| | \dfrac{df(t)}{dt} + f(t) &= t \quad \cdots (1) \\ |
| | f(0) &= 0 \quad \cdots (2) |
| | \end{cases} |
| | </math> |
| | |
| | 解答: |
| | (1)式の両辺をラプラス変換する。 |
| | <math>\mathcal{L} \bigg[ \dfrac{df(t)}{dt} \bigg] \mathcal{L} \bigg[ f(t) \bigg] = \mathcal{L} \bigg[ t \bigg]</math> |
| | ここで、<math>\mathcal{L} \bigg[ f(t) \bigg] = F(s)</math> とおいて、微分法則を適用して計算する。 |
| | |
| | <math>{sF(s) - 0} + F(s) = \dfrac{1}{s^2}</math> |
| | <math>\iff F(s) = \dfrac{1}{s^2}</math> |
| | <math>\iff F(s) = \dfrac{1}{s^{2}(s + 1)} \quad \cdots (3)</math> |
| | |
| | (3)式の右辺を部分分数展開する。 |
| | <math>\dfrac{1}{s^{2} (s + 1)} = \dfrac{A}{s} + \dfrac{B}{s^2} + \dfrac{C}{(s + 1)}</math> とおいて、A、B、Cを求める。 |
| | |
| | 両辺に <math>s^{2} (s + 1)</math> を乗算して、分子の各係数を比較する。 |
| | <math>1 = As(s + 1) + B(s + 1) + Cs^{2} = (A + C)s^{2} + (A + B)s + B \quad (4)</math> |
| | |
| | (4)式の右辺の各係数を比較すると、 |
| | <math> |
| | \begin{cases} |
| | A + C &= 0 \\ |
| | A + B &= 0 \\ |
| | B &= 1 |
| | \end{cases} |
| | </math> |
| | より、 |
| | <math>A = -1, \, \, B = 1, \, \, C = 1</math> が得られる。 |
| | |
| | したがって、以下が得られる。 |
| | <math> |
| | \begin{align} |
| | F(s) &= \dfrac{1}{s^2 (s + 1)} \\ |
| | & = - \dfrac{1}{s} + \dfrac{1}{s^2} + \dfrac{1}{s + 1} \quad \cdots (5) |
| | \end{align} |
| | </math> |
| | |
| | (5)式の両辺をラプラス逆変換して、<math>f(t) = \mathcal{L}^{-1} \bigg[ Y(s) \bigg]</math> を求める。 |
| | <math> |
| | \begin{align} |
| | \mathcal{L}^{-1} \bigg[ F(s) \bigg] &= \mathcal{L}^{-1} \bigg[ - \dfrac{1}{s} \bigg] + \mathcal{L}^{-1} \bigg[ \dfrac{1}{s^2} \bigg] + \mathcal{L}^{-1} \bigg[ \dfrac{1}{s + 1} \bigg] \\ |
| | &= -1 + t + e^{-t} |
| \end{align} | | \end{align} |
| </math> | | </math> |
概要
- ラプラス逆変換
 に対し、
に対し、 ![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  が存在するとき、
が存在するとき、![{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b87c9f1a84b5bf1a1929d9e2a7a2c616f72a045) をラプラス逆変換という。
をラプラス逆変換という。 に対し、
に対し、![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  は無数に存在する。
は無数に存在する。
- ラプラス逆変換はブロムウィチ積分で表すことができる。
- 実際にラプラス逆変換を求めるためには、変換公式を使用する。
- 部分分数展開
- ラプラス逆変換を行う際に、像関数に対して部分分数展開を適用する場合がある。
- その際には、いくつかの部分分数展開の公式を使用する。
- 公式中の対応する係数を求めるために、留数を求める方法と同様の方法を使用する。
ラプラス逆変換の定義
定義:
 に対し、
に対し、 ![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  が存在する時、
が存在する時、
![{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b87c9f1a84b5bf1a1929d9e2a7a2c616f72a045) と書き、これを
と書き、これを  のラプラス逆変換(inverse Laplace transform)という。
説明:
ラプラス変換は全単射ではないので、通常の関数の逆関数と同じようにラプラス逆変換を定義できるわけではない。
のラプラス逆変換(inverse Laplace transform)という。
説明:
ラプラス変換は全単射ではないので、通常の関数の逆関数と同じようにラプラス逆変換を定義できるわけではない。
ラプラス逆変換の定義の考え方
 に対し、
に対し、![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  が存在する場合、それらは無数に存在して1つに決まらない。
が存在する場合、それらは無数に存在して1つに決まらない。
そのような、![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  を全部まとめて1グループにして、その中から代表を1つ選んで
を全部まとめて1グループにして、その中から代表を1つ選んで ![{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b87c9f1a84b5bf1a1929d9e2a7a2c616f72a045) とする。
とする。
もし、グループの中に連続な関数が存在すれば、それを代表として選び、![{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b87c9f1a84b5bf1a1929d9e2a7a2c616f72a045) と書くことにする。
と書くことにする。
 に対し、
に対し、![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205) となる
となる  が無数に存在することは、以下の定理によって示される。
が無数に存在することは、以下の定理によって示される。
すなわち、高々有限個の不連続な点で異なる原関数たちは、同一の像関数(ラプラス変換結果)をもつ。
定理:
 と
と  は、
は、 において区分的に連続な関数であるとする。
この時、
において区分的に連続な関数であるとする。
この時、![{\displaystyle {\mathcal {L}}[f(t)]={\mathcal {L}}[g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8637094016ec49e38ddfa5122e53234e369a4f6) ならば、
ならば、 と
と  は不連続な点を除いて一致する。
このような不連続な点を除けば一致するような原関数の中に連続な関数があれば、それを代表させてラプラス逆変換の値として採用する。
は不連続な点を除いて一致する。
このような不連続な点を除けば一致するような原関数の中に連続な関数があれば、それを代表させてラプラス逆変換の値として採用する。
 において、下図の関数
において、下図の関数  、
、 、
、 のラプラス変換の値は一致する。
のラプラス変換の値は一致する。
![{\displaystyle {\mathcal {L}}[f(t)]={\mathcal {L}}[g(t)]={\mathcal {L}}[h(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb854589a48639ec085ce0dc51ae00cd1e0a420)
この中で  をラプラス逆変換の値として採用する。
をラプラス逆変換の値として採用する。
![{\displaystyle {\mathcal {L}}^{-1}[F(s)]=f(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d2e5d16478d21ff16fac8c230d3fc4c1b790031)
ブロムウィチ積分
ラプラス逆変換を、ラプラス変換の定義式のような積分式として与えることも可能である。
そのような定義式は、ブロムウィチ積分(Bromwich integral)あるいは反転公式と呼ばれる。
ブロムウィチ積分は、フーリエの積分定理を使用することにより導くことができる。
ラプラス逆変換を行う場合、通常は変換公式を使用する。
そのため、ブロムウィチ積分の定義式を使用する必要はあまり生じない。
定理:
以下のブロムウィチ積分により、像関数  から原関数
から原関数  を求めることができる。
を求めることができる。
 ここで、
ここで、 とする。
説明:
ここまでの話では変数sを実数として扱ってきた。
しかし、
とする。
説明:
ここまでの話では変数sを実数として扱ってきた。
しかし、 から
から  を求めるブロムウィチ積分ではsは複素数である。
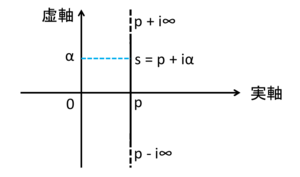
ブロムウィチ積分は、複素数平面上の虚軸に平行な直線に沿った区間
を求めるブロムウィチ積分ではsは複素数である。
ブロムウィチ積分は、複素数平面上の虚軸に平行な直線に沿った区間  から
から  の無限積分となる。
の無限積分となる。
ブロムウィチ積分:


下図に、ブロムウィチ積分の積分経路を示す。
ブロムウィチ積分は、複素数平面から時間領域への写像である。
複素数平面を用いたブロムウィチ積分は、定義通りの積分経路では計算が難しくなる。
そのため、閉曲線となるように積分経路を変更して留数(residue)を計算する。
ブロムウィチ積分の値は、複素数平面上の全ての特異点の留数の総和となる。
ラプラス逆変換公式の活用
ラプラス逆変換は、ラプラス逆変換公式を使用して計算する。
ラプラス逆変換公式は、先のラプラス逆変換の定義やブロムウィチ積分を使用して基本的な関数に対してあらかじめ求められた値を公式として表したものである。
ラプラス変換とラプラス逆変換を使用した微分方程式の解法では、そのようなラプラス逆変換公式を活用する。
ラプラス逆変換公式とラプラス変換公式は本質的に同じものである。
ラプラス逆変換公式
下表のような原関数  と像関数
と像関数  の対応関係を変換表として使用すれば、ラプラス逆変換を機械的に実行できる。
の対応関係を変換表として使用すれば、ラプラス逆変換を機械的に実行できる。

|

|
条件
|
 |
 |

|
 |
 |

|
 |
 |
 は正整数 は正整数
|
 |
 |

|
 |
 |

|
 |
 |

|
 |
 |

|
 |
 |

|
 |
 |

|
単位階段関数  |
 |

|
デルタ関数  |
 |

|
法則

|

|
条件
|
線形法則
 |
 |
|
相似法則
 |
 |
|
第1移動法則
 |
 |
|
第2移動法則
 |
 |

|
微分法則

 |

 |
|
積分法則
 |
 |
|
 積法則 積法則
 |
 |

|
合成積
 |
 |
|
 |
 |
|
 |
 |

|
 |
 |
|
ラプラス逆変換公式は、ラプラス変換公式を基にして作成されている。
ラプラス逆変換公式とラプラス変換公式は本質的に同じものであり、ラプラス逆変換公式で示されているように、ラプラス逆変換もラプラス変換と同様の性質(線形法則、移動法則、微分・積分法則、等)をもつ。
ラプラス逆変換公式における逆変換の値は、なるべく  において連続な関数を選んである。 (
において連続な関数を選んである。 ( ではどんな値でもよい)
ではどんな値でもよい)
なお、 のラプラス逆変換は
のラプラス逆変換は  でも
でも  でもよい。
でもよい。
部分分数展開
複雑な関数のラプラス逆変換を行う際、部分分数展開を使用するとうまくいく場合がある。
以下の公式における係数A、B、C、D、Eは定数とする時、A、B、C、D、Eをそれぞれ計算して求める。
- 公式 1

- 公式 2

- 公式 3

- 公式 4
分母が全てsの1次式の積の形に因数分解される場合
 は
は  の2次以下の式とする。
の2次以下の式とする。

- 公式 5
分母 = 0が多重根をもつ場合
 は
は  の3次以下の式とする。
の3次以下の式とする。

- 公式 6
分母 = 0が多重根をもち、さらにsの2次式の項も存在する場合
 は
は  の4次以下の式とする。
の4次以下の式とする。

例題 1:
部分分数展開とラプラス逆変換公式を使用することにより、以下のラプラス逆変換の値を求めよ。
![{\displaystyle {\mathcal {L}}^{-1}{\bigg [}{\frac {s}{s^{2}-4s+3}}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/060b0718424215e8c7ff91ab41c70b22d5a16fcf) 解答:
まず、
解答:
まず、 を部分分数展開する。
を部分分数展開する。

 とおいて、A, Bを求める。
Aを求める。
(1)式の両辺に
とおいて、A, Bを求める。
Aを求める。
(1)式の両辺に  を乗算すると、次式になる。
を乗算すると、次式になる。
 ここで、
ここで、 を代入すると、
を代入すると、 が得られる。
Bを求める。
(1)式の両辺に
が得られる。
Bを求める。
(1)式の両辺に  を乗算して得られた式に
を乗算して得られた式に  を代入すると、
を代入すると、 が得られる。
したがって、部分分数展開の結果は次式になる。
が得られる。
したがって、部分分数展開の結果は次式になる。
 次に、部分分数展開の結果(2)式からラプラス逆変換の値を求める。
次に、部分分数展開の結果(2)式からラプラス逆変換の値を求める。
![{\displaystyle {\begin{aligned}{\mathcal {L}}^{-1}\left[{\frac {s}{s^{2}-4s+3}}\right]&={\mathcal {L}}^{-1}\left[{\frac {3}{2}}{\frac {1}{s-3}}-{\frac {1}{2}}{\frac {1}{s-1}}\right]\qquad {\mbox{ 上 式 (2) }}\\&={\frac {3}{2}}\,{\mathcal {L}}^{-1}\left[{\frac {1}{s-3}}\right]-{\frac {1}{2}}\,{\mathcal {L}}^{-1}\left[{\frac {1}{s-1}}\right]\qquad \because {\mbox{ 線 形 法 則 }}\\&={\frac {3}{2}}e^{3t}-{\frac {1}{2}}e^{t}\qquad \because {\mbox{ 変 換 公 式 }}\\&={\frac {3e^{3t}}{2}}-{\frac {e^{t}}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3768d465cd6572fe5b891b5555a5f8f7abb43271)
例題 2:
ラプラス変換を用いて、以下の初期値問題を求めよ。
 解答:
(1)式の両辺をラプラス変換する。
解答:
(1)式の両辺をラプラス変換する。
![{\displaystyle {\mathcal {L}}{\bigg [}{\dfrac {df(t)}{dt}}{\bigg ]}{\mathcal {L}}{\bigg [}f(t){\bigg ]}={\mathcal {L}}{\bigg [}t{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24772a71dee0b46f85116c67a91c69fe4ce0bfc5) ここで、
ここで、![{\displaystyle {\mathcal {L}}{\bigg [}f(t){\bigg ]}=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e8fb4fa8d99074cad32323d00b4f994e430302) とおいて、微分法則を適用して計算する。
とおいて、微分法則を適用して計算する。


 (3)式の右辺を部分分数展開する。
(3)式の右辺を部分分数展開する。
 とおいて、A、B、Cを求める。
両辺に
とおいて、A、B、Cを求める。
両辺に  を乗算して、分子の各係数を比較する。
を乗算して、分子の各係数を比較する。
 (4)式の右辺の各係数を比較すると、
(4)式の右辺の各係数を比較すると、
 より、
より、
 が得られる。
したがって、以下が得られる。
が得られる。
したがって、以下が得られる。
 (5)式の両辺をラプラス逆変換して、
(5)式の両辺をラプラス逆変換して、![{\displaystyle f(t)={\mathcal {L}}^{-1}{\bigg [}Y(s){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f4ed6873d09ad54b6c0c5294cbcd544e7fdbe7) を求める。
を求める。
![{\displaystyle {\begin{aligned}{\mathcal {L}}^{-1}{\bigg [}F(s){\bigg ]}&={\mathcal {L}}^{-1}{\bigg [}-{\dfrac {1}{s}}{\bigg ]}+{\mathcal {L}}^{-1}{\bigg [}{\dfrac {1}{s^{2}}}{\bigg ]}+{\mathcal {L}}^{-1}{\bigg [}{\dfrac {1}{s+1}}{\bigg ]}\\&=-1+t+e^{-t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1865b2e7d4ba1af9dd4ae2d4abaed78d608a707e)

![{\displaystyle {\mathcal {L}}[f(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4213816ddd2f543bd234fd405d03df6bf0b53205)

![{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b87c9f1a84b5bf1a1929d9e2a7a2c616f72a045)


![{\displaystyle {\mathcal {L}}[f(t)]={\mathcal {L}}[g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8637094016ec49e38ddfa5122e53234e369a4f6)

![{\displaystyle {\mathcal {L}}[f(t)]={\mathcal {L}}[g(t)]={\mathcal {L}}[h(t)]=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb854589a48639ec085ce0dc51ae00cd1e0a420)

![{\displaystyle {\mathcal {L}}^{-1}[F(s)]=f(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d2e5d16478d21ff16fac8c230d3fc4c1b790031)












































































![{\displaystyle {\mathcal {L}}^{-1}{\bigg [}{\frac {s}{s^{2}-4s+3}}{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/060b0718424215e8c7ff91ab41c70b22d5a16fcf)











![{\displaystyle {\begin{aligned}{\mathcal {L}}^{-1}\left[{\frac {s}{s^{2}-4s+3}}\right]&={\mathcal {L}}^{-1}\left[{\frac {3}{2}}{\frac {1}{s-3}}-{\frac {1}{2}}{\frac {1}{s-1}}\right]\qquad {\mbox{ 上 式 (2) }}\\&={\frac {3}{2}}\,{\mathcal {L}}^{-1}\left[{\frac {1}{s-3}}\right]-{\frac {1}{2}}\,{\mathcal {L}}^{-1}\left[{\frac {1}{s-1}}\right]\qquad \because {\mbox{ 線 形 法 則 }}\\&={\frac {3}{2}}e^{3t}-{\frac {1}{2}}e^{t}\qquad \because {\mbox{ 変 換 公 式 }}\\&={\frac {3e^{3t}}{2}}-{\frac {e^{t}}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3768d465cd6572fe5b891b5555a5f8f7abb43271)

![{\displaystyle {\mathcal {L}}{\bigg [}{\dfrac {df(t)}{dt}}{\bigg ]}{\mathcal {L}}{\bigg [}f(t){\bigg ]}={\mathcal {L}}{\bigg [}t{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24772a71dee0b46f85116c67a91c69fe4ce0bfc5)
![{\displaystyle {\mathcal {L}}{\bigg [}f(t){\bigg ]}=F(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e8fb4fa8d99074cad32323d00b4f994e430302)









![{\displaystyle f(t)={\mathcal {L}}^{-1}{\bigg [}Y(s){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f4ed6873d09ad54b6c0c5294cbcd544e7fdbe7)
![{\displaystyle {\begin{aligned}{\mathcal {L}}^{-1}{\bigg [}F(s){\bigg ]}&={\mathcal {L}}^{-1}{\bigg [}-{\dfrac {1}{s}}{\bigg ]}+{\mathcal {L}}^{-1}{\bigg [}{\dfrac {1}{s^{2}}}{\bigg ]}+{\mathcal {L}}^{-1}{\bigg [}{\dfrac {1}{s+1}}{\bigg ]}\\&=-1+t+e^{-t}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1865b2e7d4ba1af9dd4ae2d4abaed78d608a707e)